2018-02-14
485
1. Исходные (неочищенные) регрессоры Х j аппроксимируются с помощью линейных уравнений регрессии в функции от выбранных инструментальных переменных {Zk}, 
.
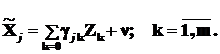(5.6)
Получаем m линейных уравнений, причем, независимых друг от друга (метод наименьших квадратов применяется m - раз). Используется классический метод наименьших квадратов. Здесь {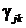 
} - матрица искомых коэффициентов; j - номер строки этой матрицы, равный номеру исходного регрессора xj; k – номер члена в (5.6), равный номеру инструментальной переменной Zk. Другими словами классический метод наименьших квадратов используется поочередно для каждого xj.
Замечание. В силу некоррелированности инструментальных переменных Zk с остатками E эти оценки получаются состоятельными:
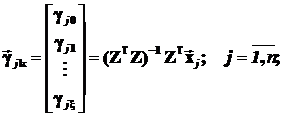(5.7)
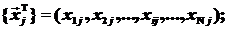(5.8)
N – число опытов; i – номер опыта;
Z – матрица планирования эксперимента, где базисные функции – линейные функции от Zk.
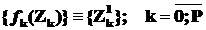
Замечание: переменные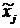 
не коррелируют с ошибками регрессии 
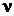, поскольку они выражаются в виде линейной комбинации некоррелирующих с E переменных {Zk}.
2. Будем рассматривать { 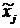} как новые инструментальные переменные для Y и аппроксимируем Y через них.
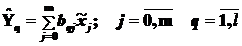(5.9)
; где q - число исходных результативных переменных.
Вектор коэффициентов для каждой фиксированной компоненты 
оцениваем снова с помощью классического метода наименьших квадратов:
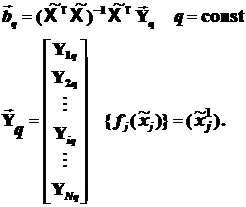
Всего получается таких l формул метода наименьших квадратов вида (5.9).
3. Поскольку все преобразования линейны, то подставляя (5.9) в (5.8) сучетом (5.6) получим выражение оценки двухшагового метода наименьших квадратов через исходные (а значит экономически интерпретируемые) инструментальные переменные Z j
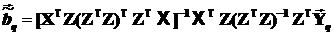(5.10)
Оценки [ bjq ] – состоятельные
Замечание: Для нелинейного МУР применимость 2х – шаговой процедуры сохраняется, однако связь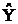 
с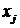 
получается уже численная. Следовательно, нужно сделать преобразование переменных перед применением 2х шагового метода наименьших квадратов
Пример: 
Вводим 
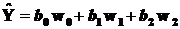
Далее 2х –шаговую процедуру можно применять по стандартной схеме к (5.6) – (5.10).
Литература
1. Айвазян С.А., Мхиторян В.С. Прикладная статистика и основы эконометрики: Учебник для ВУЗов. – М.: ЮНИТИ, 1998.
2. Букаев Г.Н., Бублик Н.Д., Горбатков С.А., Сатаров Р.Ф. Модернизация системы налогового контроля на основе нейросетевых информационных технологий. – М.: Наука, 2001.
3. Бублик Н.Д., Голичев Н.Н., Горбатков С.А., Смирнов А.В. Теоретические основы разработки технологии налогового контроля и управления. – Уфа: Изд. Башкирского государственного университета, 2004.
4. Гринченко В.Т., Мацыпура В.Т., Снарский А.А. Введение в нелинейную динамику: Хаос и фракталы. Изд. 2-е. – М.: Изд. ЛКИ, 2007.
5. Кремер Н.Ш., Путко Б.А. Эконометрика: Учебник для ВУЗов/ Под ред. Проф. Н.Ш.Кремера. – М.: ЮНИТИ-ДАНА, 2002.
6. Малинецкий Г.Г., Потапов А.Б., Подлазов А.В. Нелинейная динамика: Подходы, результаты, надежды. – М.:КомКнига, 2006.
7. Орлов А.И. Эконометрика: Учебное пособие для ВУЗов. – М.:ЭКЗАМЕН, 2007.
8. Перегудов Ф.Н, Тарасенко Ф.П. Введение в системный анализ: Учебное пособие для ВУЗов. – М.:Высшая школа, 1989.
9. Петерс Э. Хаос и порядок на рынках капитала. Новый аналитический взгляд на циклы, цены и изменчивость рынка: Пер. с англ. – М: Мир, 2000.
10. Прангишвили Н.В. Системный подход и общесистемные закономерности. – М.:СИНТЕГ, 2000.
11. Эконометрика: Учебник / Под ред. И.И. Елисеевой. – М.: Финансы и статистика, 2001.
12. Горбатков С.А., Полупанов Д.В. Методы нейроматематики в налоговом контроле. – Уфа: Изд. Башкирского государственного университета, 2008.
13. Бублик Н.Д., Голичев Н.Н., Горбатков С.А. Стохастическая оптимизация риска как ресурса вэкономических системах. – Уфа: Изд. Башкирского государственного университета, 2000.
14. Ярушкина Н.Г. Основы теории нечетких и гибридных систем. – М.: Финансы и стаистика, 2004.
15. Савицкая Г.В. Теория анализа хозяйственной деятельности: Учебное пособие. – М.: ИНФРА-М, 2006.
