Случай нелинейных координатных функций

5.5.1.Формальная замена переменных

 

Пусть 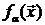 - нелинейные базовые функции в структуре модели (3.1). При этом модель линейна по параметрам  и нелинейна по .

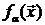Например:

 

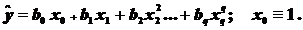                           (5.3)

 

Сделаем замену переменных

 

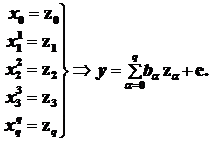                              (5.4)

 

Модель (5.4) допускает применения классической схемы метода наименьших квадратов для оценки параметров.

После нахождения 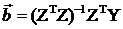, делается возврат к старым переменным.

5.5.2. Специальное преобразование

 

Пример:

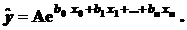
Эта модель нелинейна, как по искомым параметрам, так и по входным факторам. Требуется уже не просто замена переменных, а специальное преобразование переменных.

Например:

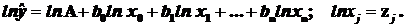
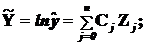
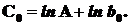
Если x₀º1, то ln b₀=0/

 

Линейные уравнения регрессии с переменной структурой.

Фиктивные переменные

 

При наличии качественных переменных имеем неоднородную структуру данных. Здесь возможны следующие подходы:

а) Построение разных (отдельных) моделей для каждого уровня качественной переменной.

б) Введение в уравнение регрессии качественных переменных. Они называются также фиктивными, номинальными, нечисловыми, структурными, “манекенами” (dummy variabls) и присвоение градациям этих переменных “цифровых меток”.

 

Возможные подходы при кодировке:

1. Введение булевых (бинарных, дихотомических переменных)

                              

 

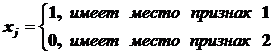
Например: “признак 1” – есть высшее образование;

 “признак 2” – нет высшего образования.

 

Случай нескольких градаций качественного признака. Если качественный признак имеет несколько уровней, то возможны два подхода:

 

1.Ввести дискретную переменную, имеющую столько же уровней, сколько признаков.

2.Ввести несколько бинарных переменных.

В примере с образованием (начальное, среднее, высшее): Х _j = (1; 2; 3;)

Однако такие данные трудно содержательно интерпретировать.

Действительно, приписываемые цифровые метки (1; 2; 3;) никак не связаны ни с экспертными оценками, ни с закономерностями исследуемого объекта. Такое кодирование вносит в уравнение регрессии искусственные связи. В частности, качественный признак “образование” может оказаться на порядок более значимым (или менее значимым) по сравнению с другими факторами в зависимости от цифр кода.

Поэтому предпочтительнее способ 2, т.е. введение нескольких бинарных переменных.

Правило: Число бинарных переменных должно быть на 1 меньше, чем число градаций качественного признака.

 

Поясним это на примере с качественным признаком “образование”. Число градаций 3, значит достаточно ввести две бинарные переменные.

 

 

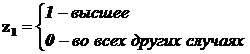
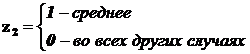
Если образование среднее, то автоматически оно не начальное.

Если начальное, то это отражено парой {Z₁=0; Z₂=0}.

Если ввести третью бинарную переменную

 

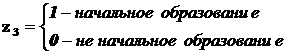
– возникает “логическая ловушка”, е сли сумма значений фиктивный переменных, включенных в регрессию, равна постоянному числу (например: 1) в любой i–ой строке, то качественный признак будет неразличим в уравнении регрессии, т.е. его оценка будет смешана со свободным членом.

 

Поясним это утверждение.

Пусть качественный признак отражен тремя градациями и, соответственно закодирован тремя бинарными (двоичными) переменными Z₁, Z₂, Z₃.

Тогда их сумма равна:

Z_i = Z₁+ Z₂+ Z₃=1

в любой i – ой строке матрицы планирования Х. Возникает функциональная мультиколлинеарность, т.е. мультиколлинеарность состоит в линейной зависимости первого столбца для 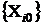с вектор – столбцами для 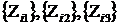, а именно: первый столбец равен сумме столбцов для качественных переменных. Тогда матрица нормальных уравнений

 

 

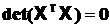
и метод наименьших квадратов неприменим.

 

Смешанные модели с влиянием качественных переменных на параметры :

Замечание 3: Возможны смешанные уравнения регрессии с фиктивными переменными в виде произведений регрессоров:

 

        (5.5)

 

Пример:

 - потребление продукта.

Х – доход

Z₁ – сезонность (влияние на свободный член)

Z₂ – уровень доходности домашнего хозяйства влияют на b ₁ при Х (склонность к потреблению).