Сравнительная оценка силы связи фактора с результатом с помощью среднего коэффициента эластичности

Коэффициент эластичности

%

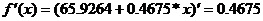
Вывод: изменение x на 1% от своей средней величины приведет к изменению y от своего среднего уровня на 0,835%.

 

4. Оценим с помощью средней ошибки аппроксимации качество уравнений.

, средняя ошибка аппроксимации не должна превышать 8-10%. Чем меньше , тем лучше качество уравнения регрессии. Если ошибка:

<8%	8%-10%	>10%
Качество хорошее	Качество удовлетворительное	Качество неудовлетворительное

 

y = 65.9264+0.4675*x

 - первая строчка в таблице;

 - вторая строчка в таблице;

 - третья строчка в таблице;

 - четвёртая строчка в таблице;

 - пятая строчка в таблице;

 - шестая строчка в таблице;

 - седьмая строчка в таблице;

 - восьмая строчка в таблице;

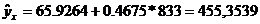 - девятая строчка в таблице;

 -десятая строчка в таблице;

 - одиннадцатая строчка в таблице;

 - двенадцатая строчка в таблице;

 - тринадцатая строчка в таблице;

A_i=

A_i=  - первая строчка в таблице;

A_i=  - вторая строчка в таблице;

A_i= 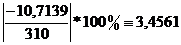 - третья строчка в таблице;

A_i=  - четвёртая строчка в таблице;

A_i=  - пятая строчка в таблице;

A_i=  - шестая строчка в таблице;

A_i=  - седьмая строчка в таблице;

A_i=  - восьмая строчка в таблице;

A_i=  - девятая строчка в таблице;

A_i=  - десятая строчка в таблице;

A_i=  - одиннадцатая строчка в таблице;

A_i=  - двенадцатая строчка в таблице;

A_i=  - тринадцатая строчка в таблице.

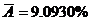
Вывод: качество уравнения удовлетворительно, так как средняя ошибка аппроксимации находится в промежутке от 8% до 10% ().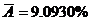

 

5. Оценим статистическую надежность результатов регрессионного моделирования с помощью F-критерия Фишера.

 - фактическое значение критерия Фишера, где n – количество исходных величин.

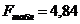(приложение стр.187,практикум по эконометрике)

24,61>4.84

Вывод: 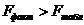, уравнение регрессии статистически значимо. Хорошее уравнение, можно пользоваться им для прогнозирования.