Молекулы газа движутся хаотически и сталкиваются между собой. Пусть λ – длина свободного пробега молекулы между двумя последовательными столкновениями; λ – случайная величина. Введём её усреднённое значение:  . Средняя продолжительность свободного пробега (среднее время между двумя последовательными столкновениями)
. Средняя продолжительность свободного пробега (среднее время между двумя последовательными столкновениями)  можно выразить через среднюю длину свободного пробега
можно выразить через среднюю длину свободного пробега  и среднюю арифметическую скорость молекул
и среднюю арифметическую скорость молекул  :
:
 . (7.1)
. (7.1)
| Рис.7.1 |

Представим траекторию молекулы как ломаную, составленную из отрезков: молекула между столкновениями летит прямолинейно и в среднем проходит путь, равный
 , а каждый излом соответствует столкновению, когда молекула меняет направление движения (рис.7.1).
, а каждый излом соответствует столкновению, когда молекула меняет направление движения (рис.7.1). Среднее число столкновений молекулы за секунду будет равно числу изломов на длине пути, равной  , так как путь, пройденный молекулой за 1 секунду, равен в среднем
, так как путь, пройденный молекулой за 1 секунду, равен в среднем  :
:
 . (7.2)
. (7.2)

| Рис.7.2 |
 и для
и для  . При этом примем следующую модель: молекулы считаем упругими шариками диаметром d. При столкновениях таких молекул их центры могут сблизиться на минимальное расстояние, равное d (рис. 7.1). Молекулы – не шарики, однако понятие эффективного диаметра для них можно ввести: эффективный диаметр молекулы
. При этом примем следующую модель: молекулы считаем упругими шариками диаметром d. При столкновениях таких молекул их центры могут сблизиться на минимальное расстояние, равное d (рис. 7.1). Молекулы – не шарики, однако понятие эффективного диаметра для них можно ввести: эффективный диаметр молекулы  – это минимальное расстояние, на которое могут сблизиться при столкновении центры двух молекул. Эффективный диаметр имеет порядок величины 10-10 м. Он немного зависит от температуры: при увеличении температуры кинетическая энергия сталкивающихся молекул больше, и приблизиться они друг к другу могут на более короткое расстояние.
– это минимальное расстояние, на которое могут сблизиться при столкновении центры двух молекул. Эффективный диаметр имеет порядок величины 10-10 м. Он немного зависит от температуры: при увеличении температуры кинетическая энергия сталкивающихся молекул больше, и приблизиться они друг к другу могут на более короткое расстояние. Введём ещё одно определение. Эффективное сечение молекулы равно
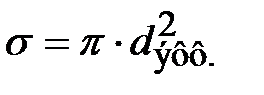 (7.3)
(7.3)
то есть площадь круга с радиусом, равным эффективному диаметру молекулы  , называется эффективным сечением. Если описать вокруг молекулы сферу радиусом
, называется эффективным сечением. Если описать вокруг молекулы сферу радиусом  , то внутрь этой сферы не сможет попасть центр другой молекулы (рис.7.3). Сечение такой сферы и есть эффективное сечение
, то внутрь этой сферы не сможет попасть центр другой молекулы (рис.7.3). Сечение такой сферы и есть эффективное сечение  .
.
Чтобы определить среднее число столкновений молекулы с другими в единицу времени  , сначала рассмотрим движение одной молекулы среди неподвижных молекул. Траектория нашей движущейся молекулы – ломаная линия. Опишем вокруг траектории цилиндр так, что ось цилиндра совпадает с траекторией молекулы, а радиус равен
, сначала рассмотрим движение одной молекулы среди неподвижных молекул. Траектория нашей движущейся молекулы – ломаная линия. Опишем вокруг траектории цилиндр так, что ось цилиндра совпадает с траекторией молекулы, а радиус равен  . Площадь его основания равна
. Площадь его основания равна  . Цилиндр – тоже ломаный (рис.7.4).
. Цилиндр – тоже ломаный (рис.7.4).
Столкновение произойдёт, если центр какой-либо молекулы попадёт в этот ломаный цилиндр. За время  путь молекулы равен
путь молекулы равен  ; это – длина цилиндра. Объём цилиндра равен
; это – длина цилиндра. Объём цилиндра равен 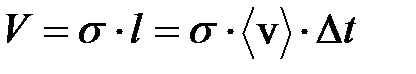 . Число молекул, центры которых попали в цилиндр, равно
. Число молекул, центры которых попали в цилиндр, равно 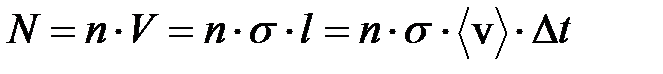 ; это и есть число столкновений нашей молекулы с другими за время
; это и есть число столкновений нашей молекулы с другими за время  . За единицу времени число столкновений будет равно
. За единицу времени число столкновений будет равно

| Рис.7.3 |

| Рис.7.4 |
 . (7.4)
. (7.4) Если молекулы движутся, в (7.4) надо заменить среднюю скорость  на среднюю относительную скорость, тогда:
на среднюю относительную скорость, тогда:
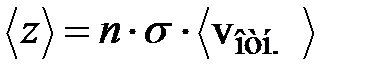 . (7.5)
. (7.5)
Относительная скорость – скорость первой молекулы относительно второй – равна:
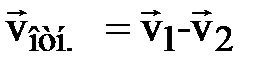 , (7.6)
, (7.6)
где 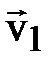 и
и  – скорости первой и второй молекул соответственно. Возведём (7.6) в квадрат и усредним:
– скорости первой и второй молекул соответственно. Возведём (7.6) в квадрат и усредним:
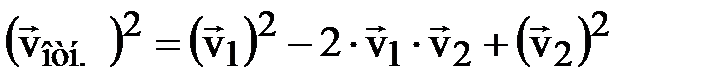

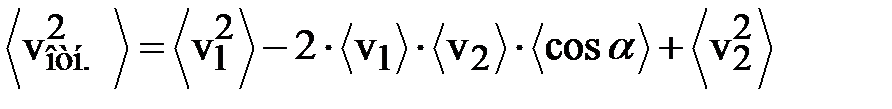
Здесь  – угол между векторами
– угол между векторами 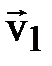 и
и  ;
;  , поскольку угол может принимать любые значения с равной вероятностью из-за хаотичности движения молекул. Кроме того,
, поскольку угол может принимать любые значения с равной вероятностью из-за хаотичности движения молекул. Кроме того,  , тогда
, тогда 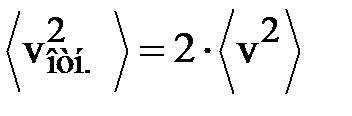 , и среднеквадратичная относительная скорость
, и среднеквадратичная относительная скорость
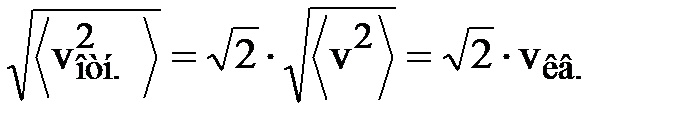 .
.
Аналогично, для средних арифметических скоростей  . Из (7.5) и (7.3) получим:
. Из (7.5) и (7.3) получим:
 . (7.7)
. (7.7)
Наконец, средняя длина свободного пробега из (7.2):
 ,
,
 , (7.8)
, (7.8)
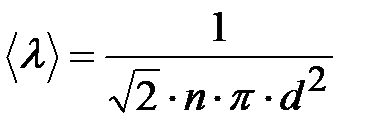 . (7.8а)
. (7.8а)
Поскольку для идеального газа  , то из (7.8)
, то из (7.8)
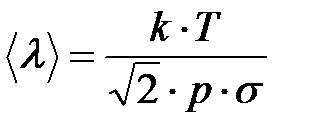 . (7.8б)
. (7.8б)
Отсюда видно, что с повышением температуры при постоянном давлении длина свободного пробега молекул растёт.
Билет
 2018-02-14
2018-02-14 760
760








