А) Коэффициент диффузии

Рис.7.5

Пусть концентрация уменьшается с координатой Z по какому-либо закону (рис.7.5). Пусть слева от площадки концентрация больше, чем справа:

Выберем малую площадку 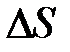, перпендикулярную оси OZ. Будем считать, что все молекулы могут двигаться только параллельно координатным осям и имеют одинаковые скорости теплового движения, равные средней арифметической . Площадку могут пересечь молекулы, которые летели по направлению к ней, а это часть всех молекул: ещё летит от площадки тоже параллельно оси OZ, и ещё по движутся параллельно двум другим осям. За время до площадки дойдут те молекулы, которые были от площадки на расстоянии не больше, чем , то есть находились в объёме . Концентрация молекул слева от площадки , поэтому число молекул, пересекающих площадку слева направо за время , равно:

. (7.17)

Аналогично, число молекул, пересекающих площадку справа налево тот же промежуток времени, равно:

. (7.18)

Результирующий перенос будет в положительном направлении оси OZ:

. (7.19)

Возникает вопрос: где именно, как далеко от площадки, нужно взять концентрации и 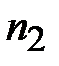? Последний раз перед пересечением площадки молекулы сталкиваются с другими молекулами и изменяют направление движения на расстоянии от площадки, равном длине свободного пробега; следовательно, они перенесут через неё информацию о концентрации, сложившуюся на расстоянии от площадки. Тогда, если функция достаточно гладкая, можно записать производную её по координате как отношение конечных приращений (см. рис.7.5):