При выводе формулы для коэффициента вязкости рассуждения аналогичны. Пусть скорость направленного движения слоёв газа убывает с координатой Z (рис.7.6). Концентрации молекул слева и справа одинаковы, и за время  площадку пересечёт одинаковое число молекул, равное
площадку пересечёт одинаковое число молекул, равное
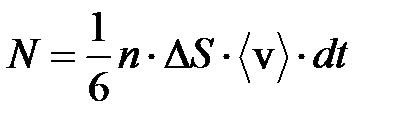 . (7.23)
. (7.23)
Импульс молекул, находящихся слева от площадки, связанный с направленным движением слоёв газа, равен 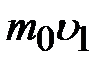 . Эти молекулы перенесут слева направо импульс суммарный
. Эти молекулы перенесут слева направо импульс суммарный 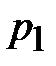 :
:
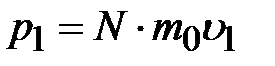 .
.
Аналогично, в обратном направлении будет перенесён импульс
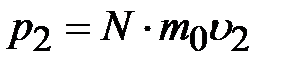 .
.
Результирующий перенос:
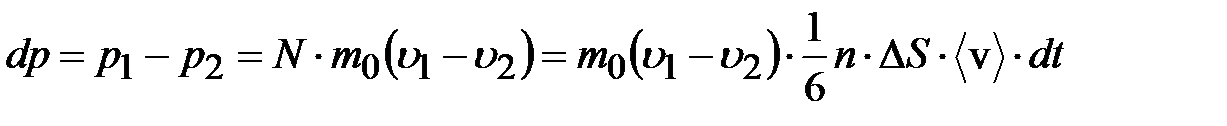 . (7.24)
. (7.24)
| Рис.7.6 |
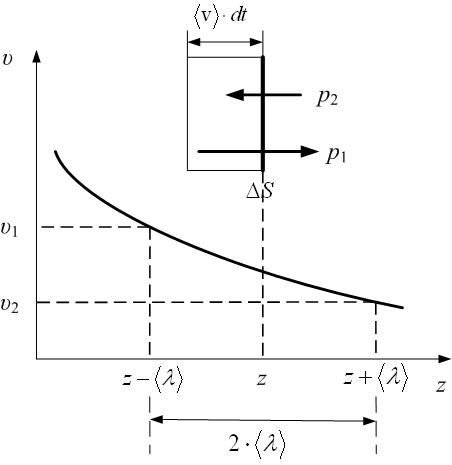
Молекулы, переходя из более быстрого слоя, движущегося со скоростью
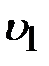 , в более медленный слой, движущийся со скоростью
, в более медленный слой, движущийся со скоростью 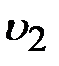 , переносят свой импульс, связанный с направленным движением слоёв, и медленный слой в целом ускоряется. Наоборот, более медленные молекулы переходят в быстрый слой и в целом его притормаживают. Это и проявляется как вязкость: скорости направленного движения слоёв выравниваются.
, переносят свой импульс, связанный с направленным движением слоёв, и медленный слой в целом ускоряется. Наоборот, более медленные молекулы переходят в быстрый слой и в целом его притормаживают. Это и проявляется как вязкость: скорости направленного движения слоёв выравниваются.
Аналогично (7.20) выразим производную  (градиент скорости направленного движения):
(градиент скорости направленного движения):
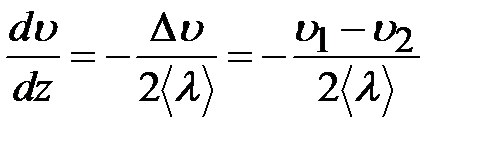 . (7.25)
. (7.25)
Молекулы, переходя через площадку, переносят через неё импульсы, связанные с теми скоростями направленного движения, которые сложились на расстоянии  от площадки. Из (7.24) и (7.25):
от площадки. Из (7.24) и (7.25):
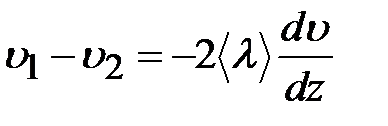 ,
,
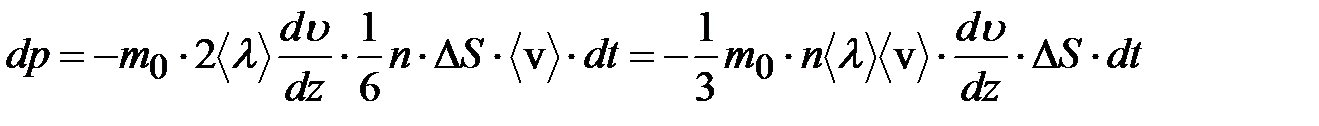 . (7.26)
. (7.26)
Сравнив (7.26) и (7.13), получим коэффициент динамической вязкости:
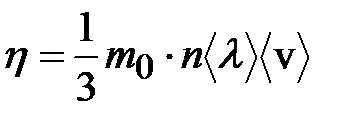 , (7.27)
, (7.27)
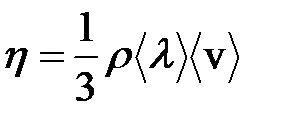 , (7.28)
, (7.28)
так как плотность  .
.
Коэффициент вязкости газа с ростом температуры при постоянном давлении растёт: и за счёт увеличения скорости хаотического движения:
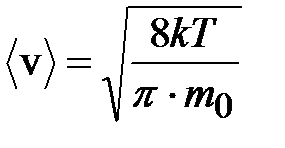 ,
,
и за счёт увеличения длины свободного пробега (7.8б): 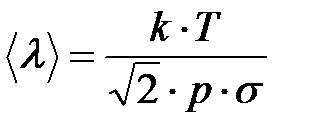 .
.
 2018-02-14
2018-02-14 371
371








