2018-02-14
943
Рассмотрим гармонические колебания, то есть колебания, происходящие по гармоническому закону (
или 
). Представим себе материальную точку М, равномерно вращающуюся по окружности радиуса А с угловой скоростью ω (рис.4.1). Тогда проекция точки М на ось х будет совершать периодические колебания вдоль оси OX:
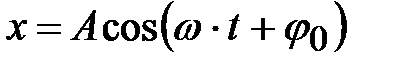, (4.1)
где А – амплитуда колебаний (абсолютное значение максимального смещения), 
– фаза колебаний, которая определяет угловое смещение точки М в любой момент времени, 
– начальная фаза, 
– круговая (циклическая) частота, равная
; (4.2)
ν – частота колебаний (число полных колебаний в единицу времени, 
, 
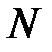– число колебаний за время t), 
– период колебаний (время совершения одного полного колебания). Выражение (4.1) – кинематическое уравнение гармонического колебательного движения.
| Рис.4.2 |
на рис.4.2 эквивалентно гармоническому колебанию.|
|
|
Ещё одно возможное представление гармонических колебаний – представление в виде комплексного числа:
. (4.3)
При этом не теряется информация о координате y точки М на рис.4.1, поскольку из (4.3) по формуле Эйлера получим:
,
или
Ещё одно преимущество записи колебания (4.3): физические задачи на колебания сводятся просто к операциям с комплексными числами.
Почему рассматриваем в первую очередь именно гармонические колебания? Ведь реальные процессы чаще описываются негармоническими функциями. По теореме Фурье любую периодическую функцию 
с периодом 
(
) можно представить в виде ряда (ряд Фурье):
, (4.4)
где
– среднее значение функции 
;
; 
.
Иными словами, любое периодическое колебание можно представить в виде суперпозиции гармонических колебаний кратных частот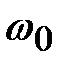 
, 
, 
, …. Частота 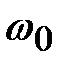называется основной частотой; 
– первый обертон и т.д.
Определение: совокупность частот и соответствующих им амплитуд называется спектром колебания. Спектр можно представить графически. Пусть – чётная:
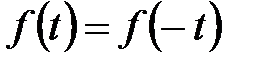
| Рис.4.3 |
| Рис.4.4 |
тогда все
: 
, и спектр состоит только из чётных гармоник (рис.4.3).
Реально можно ограничиться первыми несколькими членами ряда, если функция не очень «плохая».
Периодическая функция имеет дискретный спектр. Непериодическую тоже можно разложить по гармоническим составляющим, но это она будет иметь непрерывный спектр 
(рис.4.4), а ряд Фурье переходит в интеграл Фурье.
