Розділ 3. Методичні вказівки до розв’язання завдань з розділу «елементи векторної алгебри»

Вектори і дії з ними

Приклади розв’язування завдань

Задача № 3. Задані вектори

а) обчислити суму, різницю та скалярний добуток векторів -4 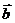і ;

б) знайти модуль векторного добутку векторів 3  і ;

в) обчислити мішаний добуток векторів , 3 , .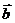

Розв’язання:

а) З’ясуємо координати векторів-4 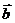і :

 

.

Обчислимо суму векторів -4 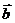і :

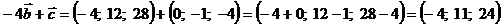
Обчислимо різницю векторів -4 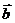і :

Обчислимо скалярний добуток векторів -4 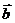і :

.

 

б) З’ясуємо координати векторів 3  і :

.

Знайдемо векторний добуток векторів 3  і :

 Обчислимо модуль векторного добутку векторів 3  і :

.

в) З’ясуємо координати векторів , 3 , :

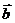Обчислимо мішаний добуток векторів , 3 , :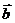

 

Відповідь: ; ; ; ; .

 

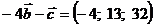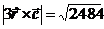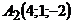
Задача № 4. Задані чотири точки , , 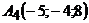. Знайти

а) кут ;

б) площу трикутника

 в) об’єм трикутної піраміди з вершинами в точках А₁, А₂, А₃, А₄;

Розв’язання:

а) Кут  будемо розглядати як кут між векторами 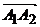 та . Знайдемо його за формулою:

Для того щоб використати вказану формулу необхідно обчислити координати векторів 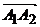 та :

,

,

Тоді

.

Таким чином кут

 

б) Трикутник  є трикутником, побудованим на векторах 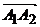 та , тому її площу  можна знайти за формулою:

.

Враховуючи, що:

,

,

 

обчислимо векторний добуток  та його модуль:

.

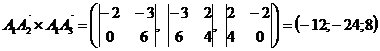
Отже,

 (кв. одиниць).

в) Трикутну піраміду з вершинами в точках А ₁, А ₂, А ₃, А ₄ будемо розглядати як піраміду, побудовану на векторах , , . Її об’єм  знайдемо за формулою:

.

З’ясуємо координати векторів , ,  :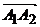

,

,

.

Знайдемо мішаний добуток  цих векторів:

.

Тоді

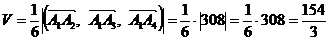 (куб. одиниць).

Відповідь: а) ; б) ; в)

 

РОЗДІЛ 4. Методичні вказівки до розв’язання завдань з розділу «Елементі аналітичної геометрії»

Пряма на площині