Розділ 5. Методичні вказівки до розв’язання завдань з розділу «вступ до математичного аналізу»

Границі

Приклади розв’язування завдань

Задача №7. Обчислити границю функції

а) ;          ;

в) 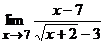;           г) ;

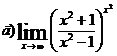
Розв’язання:

а)

 Маємо невизначеність вигляду . Розкриємо вказану невизначеність, позбавившись від так званого критичного множника. Для цього знайдемо корені квадратних тричленів  та 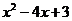, розв’язавши відповідні квадратні рівняння:

 

1)

; .

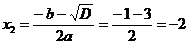 Тоді враховуючи, що

 

2)

;  

Тоді враховуючи, що

 

Отже

.

 

   

Маємо невизначеність вигляду 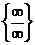. Щоб розкрити невизначеність вигляду 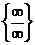, яка задана відношенням двох многочленів, треба і чисельних і знаменник розділити на найвищий степінь  у цих многочленах.

    Керуючись цим загальним прийомом, поділимо чисельник і знаменник дробу на :

 

в)

Маємо невизначеність вигляду . Розкриємо дану невизначеність помноживши чисельник та знаменник функції під знаком границі на вираз, спряжений до знаменника:

.

 

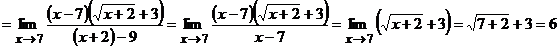г) ;

Маємо невизначеність вигляду . Розкрити її можна кількома способами.

1 спосіб.

Застосуємо формулу :

Використаємо так звану «першу чудову границю»:

Адже

.

 

Так як за «першою чудовою границею»:

.

 Крім того,

.

.

2 спосіб.

Його суть також зводиться до використання «першої чудової границі»:

.

 

Маємо невизначеність вигляду . Для розкриття невизначеностей вигляду  використовують так звану «другу чудову границю»:

.

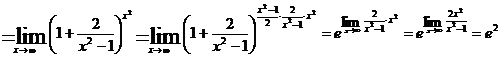
Так як за «другою чудовою границею»:

.

 Крім того,

.

Відповідь: а) ; б) 4; в) 6; г) 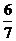; д) 2.

 

Точки розриву