Задача № 6. Задані чотири точки  ,
, 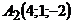 ,
,  ,
, 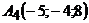 . Знайти:
. Знайти:
а) рівняння площини А1А2А3;
б) рівняння прямої А1А4;
в) відстань від точки А4 до площини А1А2А3;
г)кут між прямою А1А4 та площиною А1А2А3;
д) рівняння прямої, що проходить через точку А4 перпендикулярно площині А1А2А3;
е) рівняння площини, що проходить через точку А4 перпендикулярно до прямої А1А2.
Розв’язання:
а) Відомо координати трьох точок, які належать площині А1А2А3. Тому будемо шукати її рівняння, як рівняння площини за трьома точками  ,
,  ,
,  , тобто за формулою:
, тобто за формулою:

Складемо рівняння площини А1А2А3 за трьома точками  ,
, 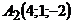 ,
,  :
:
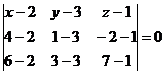




Таким чином

б) Відомо координати двох точок, які належать прямій А1А4:  ,
, 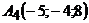 . Тому складемо рівняння прямої А1А4 за двома точками
. Тому складемо рівняння прямої А1А4 за двома точками  , тобто використовуючи формулу:
, тобто використовуючи формулу:
 .
.
Тоді


в) Відстань від точки  до площини
до площини  знаходять за формулою:
знаходять за формулою:

Тоді відстань від точки 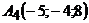 до площини
до площини  дорівнюватиме:
дорівнюватиме:
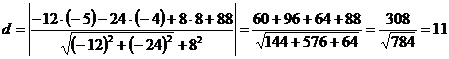 .
.
г) Кут між прямою та площиною знаходять за формулою:
 ,
,
де  - координати напрямного вектора прямої,
- координати напрямного вектора прямої,  - координати нормального вектора площини.
- координати нормального вектора площини.
Із канонічного рівняння прямої  можна знайти координати її напрямного вектора
можна знайти координати її напрямного вектора  . Тому координати напрямного вектора прямої
. Тому координати напрямного вектора прямої  дорівнюватимуть
дорівнюватимуть  .
.
Із загального рівняння площини  можна знайти координати її нормального вектора
можна знайти координати її нормального вектора  . Тому координати нормального вектора площини
. Тому координати нормального вектора площини  дорівнюватимуть
дорівнюватимуть  .
.
Знайдемо кут  між прямою
між прямою  та площиною
та площиною  знаходять за формулою:
знаходять за формулою:


д) Назвемо прямою l пряму, що проходить через точку  перпендикулярно площині А1А2А3.
перпендикулярно площині А1А2А3.
Так як пряма l є перпендикулярною до площини А1А2А3, то нормальний вектор площини А1А2А3 є напрямним вектором для прямої l, тобто  .
.
Знаючи координати цього вектора  , а також координати точки
, а також координати точки 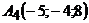 , можемо скласти рівняння прямої l за точкою
, можемо скласти рівняння прямої l за точкою  та напрямним вектором
та напрямним вектором  , тобто використовуючи формулу:
, тобто використовуючи формулу:

Тоді
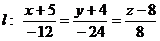
е) Назвемо 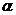 площину, що проходить через точку А4 перпендикулярно до прямої А1А2.
площину, що проходить через точку А4 перпендикулярно до прямої А1А2.
Так як пряма А1А2 є перпендикулярною до площини 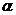 , то вектор
, то вектор  можна вважати нормальним вектором площини
можна вважати нормальним вектором площини 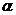 . Обчислимо координати вектора
. Обчислимо координати вектора  :
:
 , тобто
, тобто

Знаючи координати цього вектора  , а також координати точки
, а також координати точки 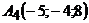 , можемо скласти рівняння площини
, можемо скласти рівняння площини  за точкою
за точкою  та нормальним вектором
та нормальним вектором  , тобто використовуючи формулу:
, тобто використовуючи формулу:

Тоді:



Відповідь: а)  ; б)
; б)  ; в)
; в) 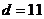 ; г)
; г)  ; д)
; д) 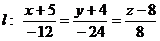 ; е)
; е)  .
.
 2018-02-14
2018-02-14 196
196








