Задача № 8. Знайти точки розриву функції, якщо вони існують, та побудувати графік цієї функції.


Розв’язання:

У кожній внутрішній точці інтервалів функція неперервна. Точками розриву можуть бути лише граничні точки інтервалів. Дослідимо їх обчисливши відповідні односторонні границі:
1) Дослідимо на неперервність точку 



Таким чином у точці  функція неперервна, так як:
функція неперервна, так як:

2) Дослідимо на неперервність точку 



Таким чином точка  є точкою розриву І-го роду, так як:
є точкою розриву І-го роду, так як:

 |

На внутрішніх точках інтервалів функція не є неперервною:

Дослідимо точку 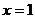 , обчисливши відповідні односторонні границі:
, обчисливши відповідні односторонні границі:


 не існує
не існує
Таким чином точка 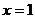 є точкою розриву ІІ-го роду.
є точкою розриву ІІ-го роду.
Точкою розриву може бути також гранична точка інтервалів. Дослідимо на неперервність точку  :
:



Таким чином у точці  є точкою розриву І-го роду, так як:
є точкою розриву І-го роду, так як:

 |
Відповідь: а) точка  є точкою розриву І-го роду заданої функції
є точкою розриву І-го роду заданої функції  ;
;
б) точка  є точкою розриву І-го роду заданої функції
є точкою розриву І-го роду заданої функції  ; точка
; точка 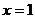 є точкою розриву І-го роду заданої функції
є точкою розриву І-го роду заданої функції  .
.
РОЗДІЛ 6. Завдання для індивідуального виконання
Задача № 1. Знайти 3∙В∙А- 2∙ВТ+4∙Е, де Е – одинична матриця третього порядку:
1. 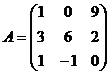 , , 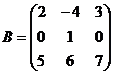
| 2.  , , 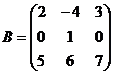
|
3. 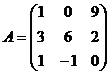 , , 
| 4.  , , 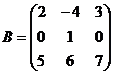
|
5. 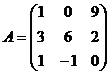 , , 
| 6.  , , 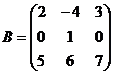
|
7. 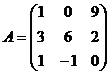 , , 
| 8.  , , 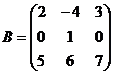
|
9. 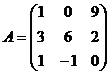 , , 
| 10.  , , 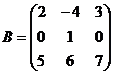
|
11. 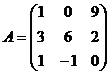 , , 
| 12.  , , 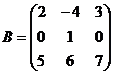
|
13. 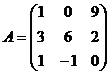 , , 
| 14.  , , 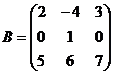
|
15. 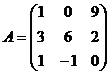 , , 
| 16.  , , 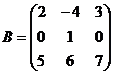
|
17. 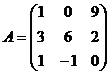 , , 
| 18.  , , 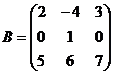
|
19. 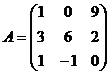 , ,  20.
20. 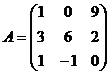 , , 
| 21. 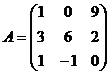 , , 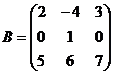 22.
22.  , , 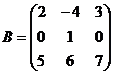
|
23. 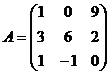 , , 
| 24.  , , 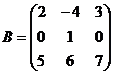
|
25.  , , 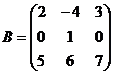
| 26.  , , 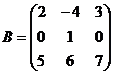
|
27. 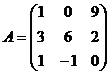 , , 
| 28.  , , 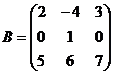
|
29. 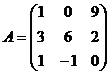 , , 
| 30.  , , 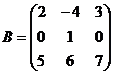
|
Задача № 2. Розв’язати систему лінійних рівнянь методом Гауса, методом Крамера та матричним методом:
1. 
| 2. 
| 3. 
|
4. 
| 5. 
| 6. 
|
7. 
| 8. 
| 9. 
|
10. 
| 11. 
| 12. 
|
13. 
| 14. 
| 15. 
|
16. 
| 17. 
| 18. 
|
19. 
| 20. 
| 21. 
|
22. 
| 23. 
| 24. 
|
25. 
| 26. 
| 27. 
|
28. 
| 29. 
| 30. 
|
Задача № 3. Задані вектори  ,
, 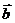 ,
,  .
.
а) обчислити суму, різницю та скалярний добуток векторів -4 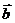 і
і  ;
;
б) знайти модуль векторного добутку векторів 3  і
і  ;
;
в) обчислити змішаний добуток векторів  , 3
, 3 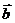 ,
,  .
.
1.  .
.
2.  .
.
3.  .
.
4.  .
.
5.  .
.
6.  .
.
7.  .
.
8.  .
.
9.  .
.
10.  .
.
11.  .
.
12.  .
.
13.  .
.
14.  .
.
15.  .
.
16.  .
.
17.  .
.
18.  .
.
19.  .
.
20.  .
.
21.  .
.
22.  .
.
23.  .
.
24.  .
.
25.  .
.
26.  .
.
27.  .
.
28.  .
.
29.  .
.
30.  .
.
Задача № 4. Задані чотири точки А1, А2, А3, А4. Знайти
а) кут  ;
;
б) площу трикутника 
в) об’єм трикутної піраміди з вершинами в точках А1, А2, А3, А4;
1.  .
.
2. 
3. 
4. 
5.  .
.
6.  .
.
7.  .
.
8.  .
.
9.  .
.
10.  .
.
11.  .
.
12.  .
.
13.  .
.
14.  .
.
15.  .
.
16.  .
.
17.  .
.
18.  .
.
19.  .
.
20.  .
.
21.  .
.
22.  .
.
23.  .
.
24.  .
.
25.  .
.
26.  .
.
27.  .
.
28.  .
.
29.  .
.
30.  .
.
Задача №5. Задані вершини трикутника АВС. Знайти:
а) рівняння та довжину сторони АВ;
б) рівняння висоти СН;
в) рівняння прямої, що проходить через точку С паралельно до сторони АВ;
г) виконати відповідні креслення до завдань а-д.
1.  2.
2.  3.
3.  4.
4.  5.
5.  6.
6.  7.
7.  8.
8.  9.
9.  10.
10.  11.
11.  12.
12.  13.
13.  14.
14.  15.
15. 
| 16.  17.
17.  18.
18.  19.
19.  20.
20.  21.
21.  .
22. .
22.  23.
23.  24.
24.  25.
25.  .
26. .
26.  27.
27.  28.
28.  29.
29.  30.
30. 
|
Задача № 6. Використовуючи дані задачі 4, знайти
а) рівняння площини А1А2А3;
б) рівняння прямої А1А4;
в) відстань від точки А4 до площини А1А2А3;
г)кут між прямою А1А4 та площиною А1А2А3;
д) рівняння прямої, що проходить через точку А4 перпендикулярно площині А1А2А3;
е) рівняння площини, що проходить через точку А4 перпендикулярно до прямої А1А2.
Задача № 7. Обчислити границі (не користуючись правилом Лопіталя):
1. 
| 
| 
|

| 
| |
2. 
| 
| 
|

| 
| |
3. 
| 
| 
|

| 
| |
4. 
| 
| 
|

| 
| |
5. 
| 
| 
|

| 
| |
6. 
| 
| 
|

| 
| |
7. 
| 
| 
|

| 
| |
8. 
| 
| 
|

| 
| |
9. 
| 
| 
|

| 
| |
10. 
| 
| 
|

| 
| |
11. 
| 
| 
|

| 
| |
12. 
| 
| 
|

| 
| |
13. 
| 
| 
|

| 
| |
14. 
| 
| 
|

| 
| |
15. 
| 
| 
|

| 
| |
16. 
| 
| 
|

| 
| |
17. 
| 
| 
|

| 
| |
18. 
| 
| 
|

| 
| |
19. 
| 
| 
|

| 
| |
20. 
| 
| 
|

| 
| |
21. 
| 
| 
|

| 
| |
22. 
| 
| 
|

| 
| |
23. 
| 
| 
|

| 
| |
24. 
| 
| 
|

| 
| |
25. 
| 
| 
|

| 
| |
26. 
| 
| 
|

| 
| |
27. 
| 
| 
|

| 
| |
28. 
| 
| 
|

| 
| |
29. 
| 
| 
|

| 
| |
30. 
| 
| 
|

| 
|
Задача № 8. Знайти точки розриву функції, якщо вони існують, та побудувати графік цієї функції.
1. 
| 16. 
|
2. 
| 17. 
|
3. 
| 18. 
|
4. 
| 19. 
|
5. 
| 20. 
|
6. 
| 21. 
|
7. 
| 22. 
|
8. 
| 23. 
|
9. 
| 24. 
|
10. 
| 25. 
|
11. 
| 26. 
|
12. 
| 27. 
|
13. 
| 28. 
|
14. 
| 29. 
|
15. 
| 30. 
|
ЛІТЕРАТУРА:
1. Вища математика: Навч.-метод. посібник для самостійного вивчення дисципліни / К.Г.Ввлєєв, І.А.Джалладова, О.І.Лютий та ін. – К.: КНЕУ, 1999. – 396 с.
2. Грисенко М.В. Математика для економістів: Методи й моделі, приклади й задачі: Навчальний посібник. – К.: Либідь, 2007. – 720 с.
3. Дубовик В.П., Юрик І.І. Вища математика: Навч. посібник. – К.: А.С.К., 2006. – 648 с.
 2018-02-14
2018-02-14 420
420







