Задача № 5. Задані вершини трикутника АВС, де 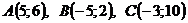 .Знайти:
.Знайти:
а) рівняння та довжину сторони АВ;
б) рівняння та довжину висоти СН;
в) рівняння прямої, що проходить через точку С паралельно до сторони АВ;
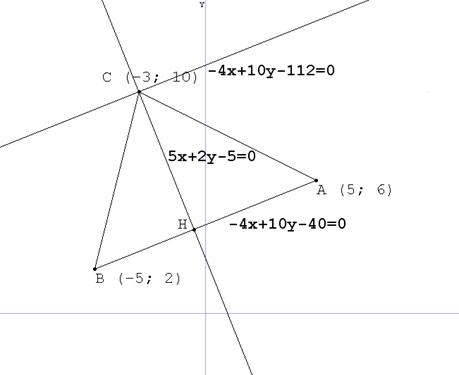
г) виконати відповідні креслення до завдань а-в.
Розв’язання:
а) Відомо координати двох точок, які належать прямій АВ: 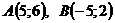 . Тому складемо рівняння прямої АВ за двома точками
. Тому складемо рівняння прямої АВ за двома точками 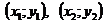 , тобто використовуючи формулу:
, тобто використовуючи формулу:
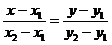 .
.
Тоді
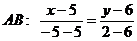
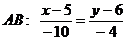
Обчислимо довжину сторони АВ, як довжину відповідного вектора 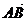 , тобто за формулою:
, тобто за формулою:
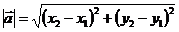 , де
, де 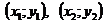 - початок і кінець вектора
- початок і кінець вектора 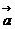 .
.
Тоді
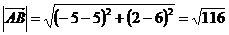
б) Пряма СН є перпендикулярною до прямої АВ. Тому нормальний вектор прямої АВ є напрямним вектором для прямої СН, тобто 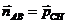 .
.
З’ясувавши координати цього вектора, а також знаючи координати точки 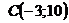 можемо скласти канонічне рівняння прямої СН за точкою
можемо скласти канонічне рівняння прямої СН за точкою 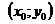 та напрямним вектором
та напрямним вектором 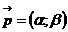 , тобто використовуючи формулу:
, тобто використовуючи формулу:
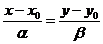
Знайдемо координати вектора 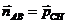 із рівняння прямої АВ, пам’ятаючи, що якщо пряма має рівняння
із рівняння прямої АВ, пам’ятаючи, що якщо пряма має рівняння 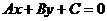 , то її нормальний вектор має координати
, то її нормальний вектор має координати 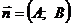 .
.
Перетворимо рівняння прямої АВ із канонічного вигляду до загального:
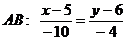
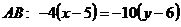
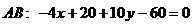
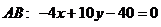 , звідки випливає, що
, звідки випливає, що 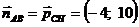 .
.
Складемо рівняння прямої СН за точкою 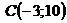 та напрямним вектором
та напрямним вектором 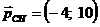 :
:
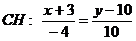
Довжину висоти СН обчислимо, як відстань від точки 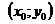 до прямою
до прямою 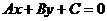 , тобто за формулою:
, тобто за формулою:
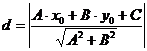
Тоді відстань від точки 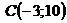 до прямою
до прямою 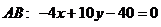 дорівнюватиме:
дорівнюватиме:
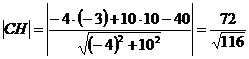 .
.
в) Пряму, що проходить через точку С паралельно до сторони АВ позначимо l. Так як пряма l є паралельною до прямої АВ, то нормальний вектор прямої АВ є нормальним вектором і для прямої l, тобто 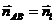 .
.
З’ясувавши координати цього вектора, а також знаючи координати точки 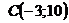 можемо скласти рівняння прямої l за точкою
можемо скласти рівняння прямої l за точкою 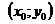 та нормальним вектором
та нормальним вектором 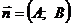 , тобто використовуючи формулу:
, тобто використовуючи формулу:
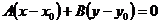
Знайдемо координати вектора 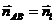 із рівняння прямої АВ:
із рівняння прямої АВ:
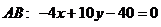 , тому
, тому 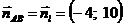 .
.
Складемо рівняння прямої l за точкою 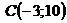 та нормальним вектором
та нормальним вектором 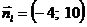 :
:
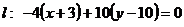
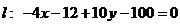
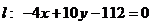
г)
 |
Відповідь: а) 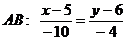 ;
; 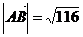 ; б)
; б) 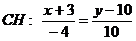 ;
; 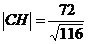 ; в)
; в) 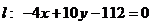 .
.
Прямі та площини у просторі
 2018-02-14
2018-02-14 265
265








