Задача 2. Розв’язати систему лінійних алгебраїчних рівнянь а) методом Крамера; б) матричним методом; в) методом Гаусса.
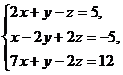
Розв’язання:
а) Розв’яжемо систему методом Крамера. Основна матриця системи та матриця-стовпець вільних членів відповідно мають вигляд:
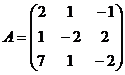 ,
, 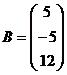 .
.
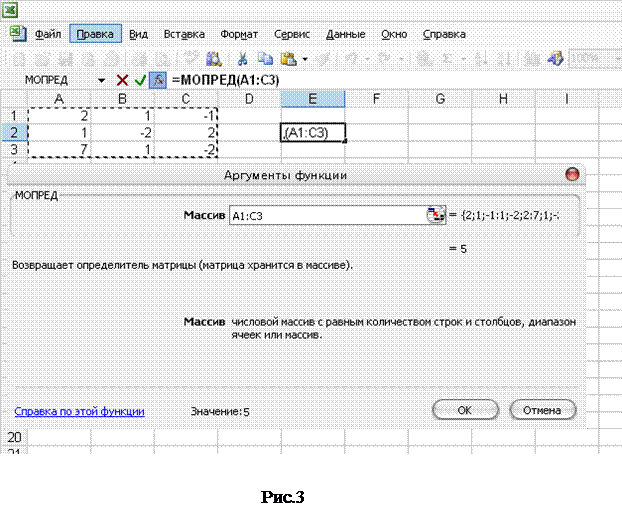
Обчислимо визначник 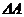 основної матриці А за відповідними правилами або використовуючи програмний засіб Microsoft Office Excel (рис. 3):
основної матриці А за відповідними правилами або використовуючи програмний засіб Microsoft Office Excel (рис. 3):

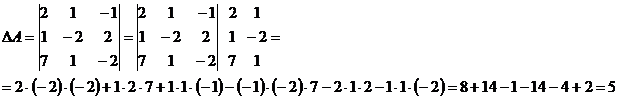
Матриця А не є виродженою(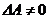 ), тому розв’язок системи можемо знайти за формулами Крамера:
), тому розв’язок системи можемо знайти за формулами Крамера:
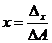 ,
, 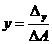 ,
, 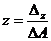 , де
, де
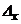 - визначник, який отримується з визначника основної матриці
- визначник, який отримується з визначника основної матриці 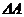 заміною першого її стовпця стовпцем вільних членів;
заміною першого її стовпця стовпцем вільних членів;
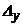 - визначник, який отримується з визначника основної матриці
- визначник, який отримується з визначника основної матриці 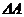 заміною другого її стовпця стовпцем вільних членів;
заміною другого її стовпця стовпцем вільних членів;
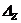 - визначник, який отримується з визначника основної матриці
- визначник, який отримується з визначника основної матриці 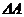 заміною третього її стовпця стовпцем вільних членів.
заміною третього її стовпця стовпцем вільних членів.
Обчислимо визначники 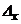 ,
, 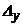 ,
, 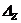 за відповідними правилами або використовуючи програмний засіб Microsoft Office Excel:
за відповідними правилами або використовуючи програмний засіб Microsoft Office Excel:
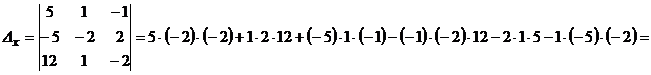
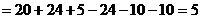 .
.
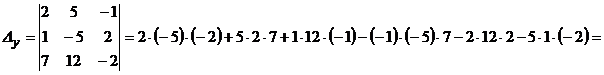
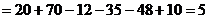 .
.
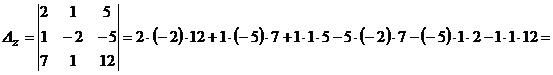
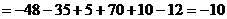 .
.
Тоді за формулами Крамера отримуємо:
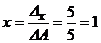 ,
, 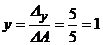 ,
, 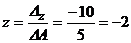 .
.
б) Розв’яжемо систему матричним методом. Дана система лінійних алгебраїчних рівнянь рівносильна матричному рівнянню
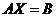 , де
, де 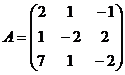 ,
, 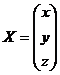 ,
, 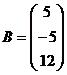
Вказане матричне рівняння (а відповідно і система лінійних алгебраїчних рівнянь) при не виродженій матриці А (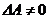 ) має розв’язок:
) має розв’язок:
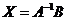 ,
,
де 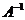 - матриця обернена до матриці
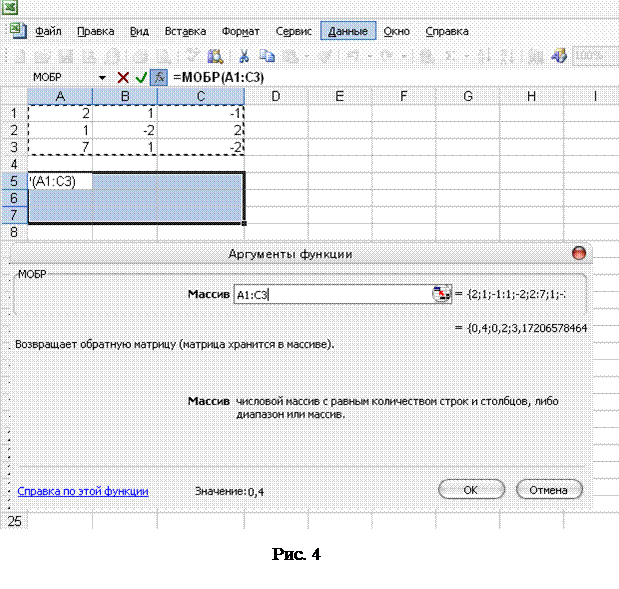
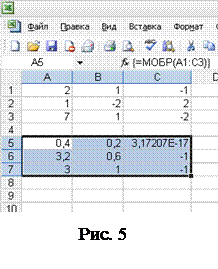
- матриця обернена до матриці 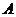 , її знаходять за формулою наведеною нижче або використовуючи програмний засіб Microsoft Office Excel (рис. 4-5):
, її знаходять за формулою наведеною нижче або використовуючи програмний засіб Microsoft Office Excel (рис. 4-5):
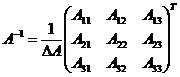
Обчислимо алгебраїчні доповнення елементів матриці А:
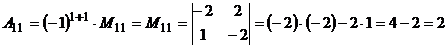 ,
, 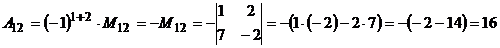 ,
, 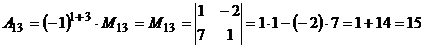 ,
,
 ,
,
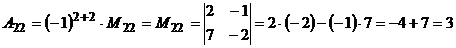 ,
,
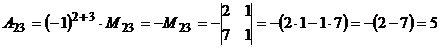 ,
,
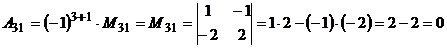 ,
,
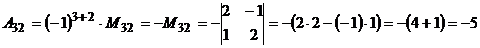 ,
,
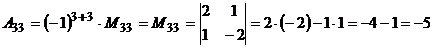 .
.
Отже 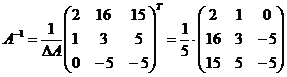 .
.
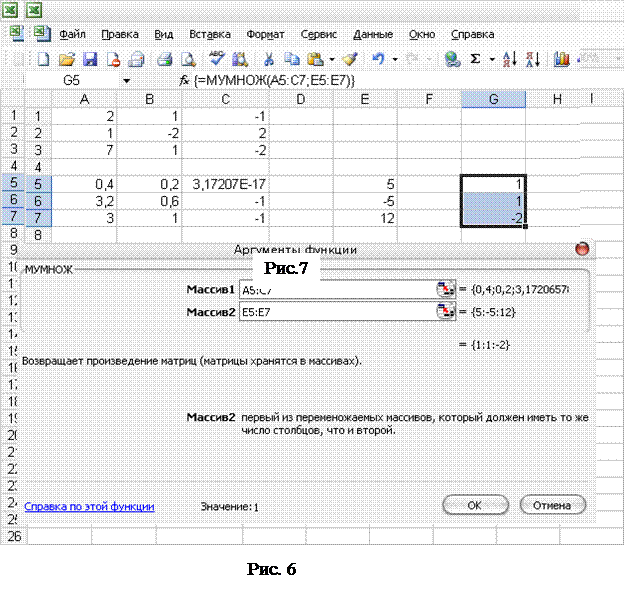
Тоді перемноживши відповідні матриці за відповідними правилами або використовуючи програмний засіб Microsoft Office Excel (рис. 6-7) отримаємо остаточний результат:
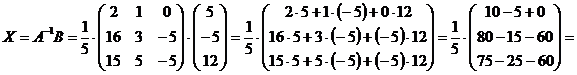
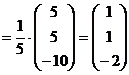 , звідки
, звідки 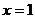 ,
, 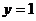 ,
, 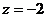 .
.
в) Розв’яжемо систему методом Гаусса. Для цього виконаємо над системою декілька елементарних перетворень, з метою зведення її до трикутного вигляду. Елементарні перетворення зручніше виконувати над відповідною розширеною матрицею системи:
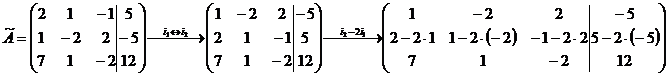
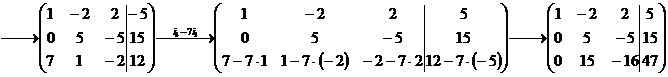
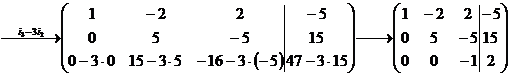
Обернений хід метода Гаусса можна провести продовжуючи виконувати елементарні перетворення над розширеною матрицею системи, з метою зведення основної матриці до одиничної:
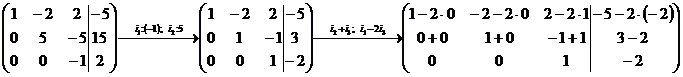
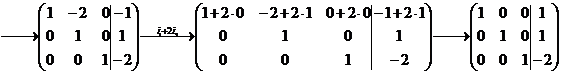
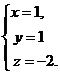
Відповідь: 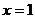 ,
, 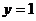 ,
, 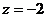 .
.
 2018-02-14
2018-02-14 368
368








