2018-02-14
1126
Постановка задачи №2
Торговая компаниярасполагает семью магазинами типа «Промтовары» (для справки: этот тип в соответствии с /2, ГОСТ/ - п редприятие розничной торговли, реализующее непродовольственные товары узкого ассортимента, основные из которых швейные и трикотажные изделия, обувь, галантерея, парфюмерия торговой площадью от 18 м2).
Компании планирует построить 8-й магазин с торговой площадью 1100 м2, для чего она разрабатывает бизнес-план и, в частности, эконометрическую модель магазина.
На этой модели специалисты должны исследовать зависимость объема продаж (у - в десятках тыс.руб./день) от размера торговой площади (х1 – в сотнях м2) и от размера паркинга (х2 в десятках автомашин)
Единицы измерения выбраны с учетом достоверности данных и удобства вычислений.
Решение задачи №2
1) Нанести в координатах х2у точки на плоскость (построить корреляционное поле).
Решение. Для наглядности выберем наши данные из таблиц 1.2-1.7. Из рисунке 3.1 видно, что прямая линия хорошо аппроксимирует связь между у и х2. Эта связь прямая и очень тесная.
|
|
|
2) Записать для своего варианта матрицу Х значений объясняющих переменных (матрицу плана).
Решение. См.среднюю матрицу в п.4.
3) Записать транспонированную матрицу плана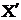 
.
Решение. См. левую матрицу в п.4.
| у | 
| ||||||
| 15 | 
| ||||||
| |||||||
| 12 | |||||||
| 9 | |||||||
| |||||||
| 6 | 
| 
| |||||
 
| |||||||
| 3 | |||||||
| 
| х2 | |||||
| 1 | 2 | 3 | 4 | 5 | 6 |
Рисунок 3.1
4) Найти произведение матриц 
.
Решение.
5) Найти обратную матрицу ()-1.
Решение. Для краткости введем обозначение: А= . требуется найти обратную матрицу А-1. Используем формулу:
где 
- определитель матрицы А,
– транспонированная матрица, составленная из алгебраических дополнений матрицы А.
=7×120×79+24×96×21+21×96×24-21×120×21-96×96×7-79×24×24=192.
Находим алгебраические дополнения:
| А11=120×79–96×96=264; | А12=-(24×79–96×21) =120; |
| А13=24×96–120×21=-216; | А21=-(24×79–21×96)=120; |
| А22=7×79-21×21=112; | А23=-(7×96–24×21)=-168; |
| А31=24×96–21×120=-216; | А32=-(7×96–21×24)=-168; |
| А33=7×120–24×24=264. |
Обратная матрица:
Проверка. Если расчеты верны, то должно выполниться равенство:
А А-1 = Е.
Для повышения точности множитель 1/192 введем отдельно.
Равенство выполнено, значит, расчет обратной матрицы выполнен верно.
|
|
|
6) Найти произведение матриц 
.
Решение.
7) Найти уравнение регрессии Y по Х1 и Х2 в форме 
=b0+ b1 х1 + +b2х2 методом наименьших квадратов путем умножения матрицы ()-1 на матрицу , т.е. рассчитать коэффициенты регрессии по формуле b=()-1 .
Решение.
Итак, ответ: b0 = -0,88; b1 =0,50; b2 = 1,63. Уравнение множественной регрессии имеет вид: = -0,88 + 0,50x1 + 1,63x2.
8) Объяснить смысл изменения значения коэффициента регрессии b1.
Решение. В задаче №1 значение b1=1,54, а теперь его значение снизилось до b1=0,50. Это связано с тем, что на объем продаж помимо торговой площади теперь влияет учитываемая площадь паркинга.
9) Рассчитать значения коэффициентов эластичности для обоих факторов и сравнить влияние каждого из них на средний объем продаж.
Решение. Коэффициент эластичности в общем случае есть функция объясняющей переменной, например: 
Если 
то 
при увеличении х1 от среднего на 1% объем продаж возрастет на 0,30%. Аналогично 
при увеличении х2 от среднего на 1% объем продаж возрастет на 0,86%.
10) Оценить аналитически прогнозное среднее значение объема продаж для проектируемого магазина "СИ" с торговой площадью х1=11 (1100 м2) и паркинговой площадью х2=8 (80 автомашин).
Решение. Объем продаж рассчитаем по уравнению регрессии:
= -0,88 + 0,50 × 11 + 1,63 × 8 = 17,66.
11.а) Найти 95%-ный доверительный интервал для среднего прогнозного значения объема продаж магазина "СИ".
Решение. По условию нужно оценить значение Мх(Y), где вектор переменных 
. Выборочной оценкой условного МOМх(Y) является значение регрессии (11, 8) = 17,66. Для построения доверительного интервала для Мх(Y) нужно знать дисперсию оценки 
и дисперсию возмущений s2:
Для удобства вычислений составим таблицу 3.1.
Таблица 3.1
| i | xi1 | xi2 | yi | 
| ei | 
|
| 1 | 1 | 1 | 2 | 1,25 | 0,75 | 0,56 |
| 2 | 1 | 2 | 3 | 2,88 | 0,12 | 0,02 |
| 3 | 2 | 2 | 4 | 3.38 | 0,62 | 0,39 |
| 4 | 3 | 3 | 5 | 5.51 | -0,51 | 0,26 |
| 5 | 4 | 3 | 5 | 6,01 | -1,01 | 1,02 |
| 6 | 5 | 4 | 7 | 8,14 | -1,14 | 1,30 |
| 7 | 8 | 6 | 14 | 12,90 | 1,10 | 1,21 |
| ∑ | 24 | 21 | 40 | 40,07 | -0,07 | 4,76 |
На основе табличных данных:
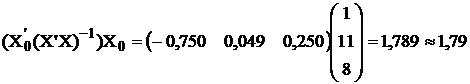
По табл.П2 находим критическое значение статистики Стьюдента t0,95; 7-2-1=5 = 2,78. Полуинтервал D = t0,95; 5∙ 
= 2,78 × 1,46 = 4,05.
Нижняя граница интервала: min = Xo - D = 17,66 - 4,05 = 13,61.
Верхняя граница интервала: mах = Xo + D = 17,66 + 4,05 = 21,71. Окончательно доверительный интервал для среднего прогнозного значения Xo: 13,61 £ МХo(Y) £ 21,71. Интервал большой, что объясняется слишком короткой выборкой.
11.б) Найти 95%-ный доверительный интервал для индивидуального прогнозного значения объема продаж магазина "СИ" 
.
Решение. Интервал рассчитаем по выражению:
где 
Полуинтервал D= 2,78 × 1,82 = 5,06. Нижние и верхние границы интервала: 
min = 17,66 - 5,06 = 12,60 и max = 17,66 + 5,06 = 22,72. Окончательно интервал имеет вид: 12,60 £ £ 22,72. Как и следовало ожидать, данный индивидуальный интервал больше предыдущего среднего.
12) Проверить значимость коэффициентов регрессии.
Решение. Стандартная ошибка рассчитывается по формуле:
где выражение под корнем есть диагональный элемент матрицы 
-1.
Отсюда: sb1 = 1,09 
= 1,28; sb2 =1,09 
= 0,83.
Так как t = çb1ç/ sb1 = 0,50/1,28 = 0,39 <t0,95;4 = 2,78, то коэффициент b1 незначим (незначимо отличается от нуля).
Так как t = çb2ç/ sb2 = 1,63/0,83 = 1,96 <t0,95;4 = 2,78, то и коэффициент b2незначим на 5%-ном уровне.
13) Найти с надежностью 0,95 интервальные оценки коэффициентов регрессии b1 и b2 и дисперсии s2.
Решение. Интервалы коэффициентов регрессии рассчитываются по формуле:bj+ t1-a,n-p-1sbj£bj£bj + t1-a,n-p-1sbj.
Поскольку оба коэффициента регрессии незначимы, то не имеет смысла строить для них доверительные интервалы.
14) Определить множественный коэффициент детерминации и проверить значимость уравнения регрессии на уровне a=0,05.
Решение. Коэффициент детерминации рассчитывается по формуле:
|
|
|
; 
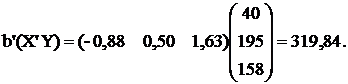
Уравнение регрессии значимо, если справедливо неравенство (критерий Фишера):
F = R2 (n-p-1)/(1- R2) p > Fa;k1;k2.
Отсюда F = 0,96(7-2-1)/(1-0,962)2 = 24,62 > F0,05;2;4.
Вывод: уравнение значимо.
15) Определить, существенно ли увеличилось значение коэффициента детерминации при введении в регрессию второй объясняющей переменной.
Решение. Значения коэффициентов детерминации для регрессий с одной и с двумя объясняющими переменными соответственно равны: R2 = 0,97 и R2 = 0,96. Увеличения значения не произошло. Введение второй переменной не увеличило адекватность модели.
