Аппроксимация. Метод наименьших квадратов

Основная задача аппроксимации — построение приближенной (аппроксимирующей) функции, в целом наиболее близко проходящей около данных точек или около данной непрерывной функции. Такая задача возникает при наличии погрешности в исходных данных (в этом случае нецелесообразно проводить функцию точно через все точки, как в интерполяции) или при желании получить упрощенное математическое описание сложной или неизвестной зависимости.

Близость исходной и аппроксимирующей функций определяется числовой мерой — критерием аппроксимации (близости). Наибольшее распространение получил квадратичный критерий, равный сумме квадратов отклонений расчетных значений от “экспериментальных” (т.е. заданных), — критерий близости в заданных точках:

Здесь — заданные табличные значения функции;

расчетные значения по аппроксимирующей функции; — весовые коэффициенты, учитывающие относительную важность i-й точки (увеличение приводит при стремлении уменьшить R к уменьшению прежде всего отклонения в i-й точке, так как это отклонение искусственно увеличено за счет относительно большого значения весового коэффициента).

Квадратичный критерий обладает рядом “хороших” свойств, таких, как дифференцируемость, обеспечение единственного решения задачи аппроксимации при полиномиальных аппроксимирующих функциях.

Другим распространенным критерием близости является следующий:

Этот критерий менее распространен в связи с аналитическими и вычислительными трудностями, связанными с отсутствием гладкости функции и ее дифференцируемости.

В обоих рассмотренных случаях в качестве значения функции , можно брать не только абсолютные, но и относительные значения, например, и др.

Выделяют две основные задачи:

-получение аппроксимирующей функции, описывающей имеющиеся данные, с погрешностью не хуже заданной;

-получение аппроксимирующей функции заданной структуры с наилучшей возможной погрешностью.

Чаще всего первая задача сводится ко второй перебором различных аппроксимирующих функций и последующим выбором наилучшей.

Основные методы. Метод наименьших квадратов.

Метод базируется на применении в качестве критерия близости суммы квадратов отклонений заданных и расчетных значений. При заданной структуре аппроксимирующей функции (х) необходимо таким образом подобрать параметры этой функции, чтобы получить наименьшее значение критерия близости, т.е. наилучшую аппроксимацию. Рассмотрим путь нахождения этих параметров на примере полиномиальной функции одной переменной:

Запишем выражение критерия аппроксимации при βi =1 (i= 1, 2,..., n) для полиномиальногоy_i^расчет(х):

Искомые переменные можно найти из необходимого условия минимума R по этим переменным, т.е. dR / da_p =0 (для р = О, 1, 2,…. к). Продифференцируем по а_р (р — текущий индекс):

Значения индексов суммирования для простоты опущены.

После очевидных преобразований (сокращение на два, раскрытие скобок, изменение порядка суммирования) получим

Получилась система n+1 уравнений с таким же количеством неизвестных , причем линейная относительно этих переменных. Эта система называется системой нормальных уравнений. Из ее решения находятся параметры a_J аппроксимирующей функции, обеспечивающие min R, т.е. наилучшее возможное квадратичное приближение. Зная коэффициенты, можно (если нужно) вычислить и величину R (например, для сравнения различных аппроксимирующих функций). Следует помнить, что при изменении даже одного значения исходных данных (или пары значений x_iу_i или одного из них) все коэффициенты изменят в общем случае свои значения, так как они полностью определяются исходными данными. Поэтому при повторении аппроксимации с несколько изменившимися данными (например, вследствие погрешностей измерения, помех, влияния неучтенных факторов и т.п.) получится другая аппроксимирующая функция, отличающаяся коэффициентами. Обратим внимание на то, что коэффициенты а_i полинома находятся из решения системы уравнений, т.е. они связаны между собой. Это приводит к тому, что если какой-то коэффициент вследствие его малости захочется отбросить, придется пересчитывать заново оставшиеся. Можно рассчитать количественные оценки тесноты связи коэффициентов. Существует специальная теория планирования экспериментов, которая позволяет обосновать и рассчитать значения х_i используемые для аппроксимации, чтобы получить заданные свойства коэффициентов (несвязанность, минимальная дисперсия коэффициентов и т.д.) или аппроксимирующей функции (равная точность описания реальной зависимости в различных направлениях, минимальная дисперсия предсказания значения функции и т.д.).

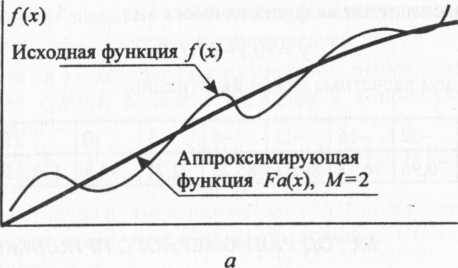
В случае постановки другой задачи — найти аппроксимирующую функцию, обеспечивающую погрешность не хуже заданной, — необходимо подбирать и структуру этой функции. Эта задача значительно сложнее предыдущей (найти параметры аппроксимирующей функции заданной структуры, обеспечивающей наилучшую возможную погрешность) и решается в основном путем перебора различных функций и сравнения получающихся мер близости. Для примера на рис. 3 приведены для визуального сравнения исходная и аппроксимирующие функции с различной степенью полинома, т.е. функции с различной структурой. Не следует забывать, что с повышением точности аппроксимации растет и сложность функции (при полиномиальных аппроксимирующих функциях), что делает ее менее удобной при использовании.

Пример.

Необходимо найти аппроксимирующую функцию в виде линейного полинома у = а₀ + а₁х по имеющимся экспериментальным данным

X	-26	-22	-16	-11	-5	3	10	25	42
У	66,7	71,0	76,3	80,6	85,7	92,9	99,4	113,6	125,1

Система нормальных уравнений будет выглядеть следующим образом:

Решим полученную систему линейных уравнений относительно а₀ и а,, получим а₀ =90,1, а₁ = 0,87.

б

Рис. 3. Влияние степени аппроксимирующего полинома М на точность аппроксимации: а — М= 2, б — М = 3,в— М=5.

Аппроксимирующая функция имеет вид у =90,1 +0,87x. Приведем расчетные значения функции:

X -26 -22 -16 -11 -5 3 10 25 42

У 64,97 70,96 76,18 80,53 85,75 92,71 98,8 111,85 126,64