Вычисление интегралов встречается при моделировании достаточно часто. Численные методы обычно применяются при взятии неберущихся интегралов от достаточно сложных функций, которые предварительно табулируются, или при интегрировании таблично заданных функций, что в экономических приложениях встречается значительно чаще.
Концепция численного интегрирования.
Все численные методы строятся на том, что подынтегральная функция приближенно заменяется более простой (горизонтальной или наклонной прямой, параболой 2-го, 3-го или более высокого порядка), от которой интеграл легко берется. В результате получаются формулы интегрирования, называемые квадратурными, в виде взвешенной суммы ординат подынтегральной функции в отдельных точках:

Чем меньше интервалы, на которых производят замену, тем точнее вычисляется интеграл. Поэтому исходный отрезок [а, b]для повышения точности делят на несколько равных или неравных интервалов, на каждом из которых применяют формулу интегрирования, а затем складывают результаты.
В большинстве случаев погрешность численного интегрирования определяется путем двойного интегрирования: с исходным шагом (шаг определяется путем равномерного деления отрезка b-а на число отрезков n\h=(b-a)/n)u c шагом, увеличенным в 2 раза. Разница вычисленных значений интегралов определяет погрешность.
Сравнение эффективности различных методов проводится по степени полинома, который данным методом интегрируется точно, без ошибки. Чем выше степень такого полинома, тем выше точность метода, тем он эффективнее.
К простейшим методам можно отнести методы прямоугольников (левых и правых) и трапеций. В первом случае подынтегральная функция заменяется горизонтальной прямой (у = с0) со значением ординаты, т.е. значения функции соответственно слева или справа участка, во втором случае — наклонной прямой (у =с1х + с0). Формулы интегрирования при разбиении отрезка [а, b] на n частей с равномерным шагом h соответственно приобретают вид:
• для одного участка интегрирования:

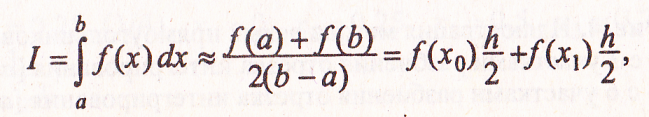
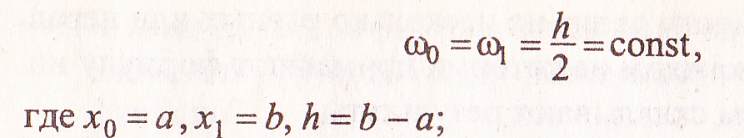

• для п участков интегрирования:
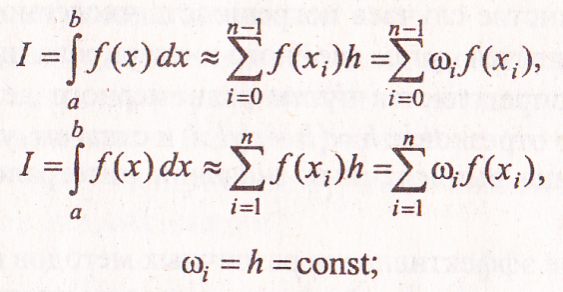

Нетрудно заметить, что в методе прямоугольников интеграл вычислится абсолютно точно только при f (х) = с (const), а в методе трапеций — при f (x) линейной или кусочно-линейной.
На рис. 4 для сравнения приведены примеры прямоугольников при различном числе участков. Наглядно видно, что площадь всех прямоугольников на правом рисунке меньше отличается от площади под кривой f(x), чем на левом.

а bab
| Рис. 5. Иллюстрация метода трапеций |
а — с 3 участками разбиения отрезка интегрирования [а, b];
б — с 6 участками разбиения отрезка интегрирования [а, b]
Метод прямоугольников не находит практического применения в силу значительных погрешностей, что тоже видно из рис. 4.
На рис. 5 приведен пример вычисления интеграла методом трапеций. По сравнению с методом прямоугольников метод трапеций более точный, так как трапеция точнее заменяет соответствующую криволинейнуютрапецию, чем прямоугольник. Рис 5.

 Погрешность R вычисления интеграла методом трапеций при использовании двойного просчета на практике может быть определена из следующего соотношения:
Погрешность R вычисления интеграла методом трапеций при использовании двойного просчета на практике может быть определена из следующего соотношения:
где In и Iп/2 — соответственно значения интеграла при числе разбиений п и п/2. Существуют и аналитические выражения для определения погрешности, но они требуют знания второй производной подынтегральной функции, поэтому имеют только теоретическое значение. С использованием двойного просчета можно организовать автоматический подбор шага интегрирования (т.е. числа разбиений n) для обеспечения заданной погрешности интегрирования (последовательно удваивая шаг и контролируя погрешность).

Получим методом левых прямоугольников:
Получим методом левых прямоугольников:

Получим методом правых прямоугольников:
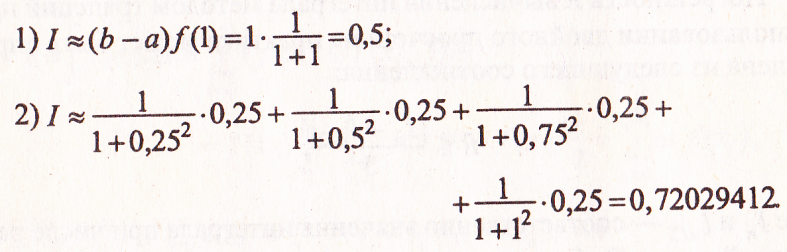
Получим методом трапеций:

 2018-02-20
2018-02-20 3521
3521
