Функції комплексної змінної

Якщо задано закон , згідно з яким кожному значенню , яке належить множині , відповідає певне значення , то кажуть, що задана однозначна функція , яка визначена на та набуває значень в . Якщо значенню відповідає декілька значень , то функція є багатозначною.

Функцію комплексної змінної можна записати у вигляді

де та – функції дійсних змінних та .

Існування границі функції комплексної змінної еквівалентне одночасному існуванню границь дійсної та уявної частин та . Аналогічно неперервність функції 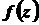у точці еквівалентна неперервності функцій та у точці .

Функція, неперервна у кожній точці області , називається неперервною у цій області.

Елементарні функції комплексної змінної. Введемо показникову функцію комплексної змінної за правилом

Тригонометричні та гіперболічні функції зв’язані з показниковою співвідношеннями

; ; ; ;

.; .

Функції, які введені за цими формулами, по-перше, для дійсних значень аргумента співпадають з відповідними функціями дійсної змінної, та, по-друге, зберігають всі властивості функцій дійсної змінної.