Диференційовність функцій. Умови Коші-Рімана

    Околом точки 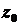 називається внутрішність деякого круга на комплексній площині з центром у вказаній точці, тобто множина , .

    Функція 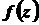, яка визначена у деякому околі точки 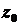, називається диференційовною у цій точці, якщо існує скінченна границя

,

яку називають похідною від функції 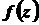 в точці .

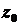    Функція  є диференційовною в точці  тоді та тільки тоді, коли виконуються умови Коші-Рімана

               ,   ,

при цьому

    .

    Однозначну функцію 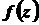, яка у всіх точках деякої області є неперервно диференційовною (має неперервну похідну), називають аналітичною (регулярною) в цій області.

    Однозначні елементарні функції є аналітичними.

    Елементарні функції комплексної змінної можна диференціювати за тими ж формулами, що і функції дійсної змінної.