Особливі точки. Лишки

 

Функція 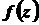, аналітична у внутрішніх точках круга , може бути представлена у цьому крузі збіжним степеневим рядом , який називається рядом Тейлора.

Для елементарних функцій комплексної змінної зберігаються розвинення у ряди Тейлора та Маклорена, отримані для функцій дійсної змінної:

, ;

, ;

, ;

, ;

, ;

,    тощо.

    Якщо функція 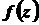 є аналітичною у кільці , то вона може бути представлена у точках цього кільця своїм рядом Лорана

,

де  , , інтегрування виконується вздовж кола , .

Радіуси  та  зв’язані з коефіцієнтами Лорана співвідношеннями

та .

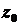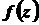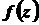    Точка  називається ізольованою особливою точкою функції , якщо  не визначена, та існує окіл , в якому функція  є аналітичною. Особлива точка  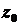називається

– усувною, якщо існує скінчений ;

– полюсом, якщо ;

– істотно особливою точкою, якщо  не існує.

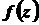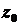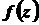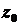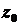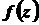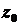Число  називається порядком нуля функції  в точці , якщо функція  аналітична в точці  , , та . Якщо точка  є нулем порядку  для функції , то вона є полюсом порядку  для функції . Зокрема, число  є полюсом порядку  для функції , якщо .

    Якщо особлива точка 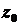є усувною, всі коефіцієнти головної частини відповідного ряду Лорана дорівнюють нулю, у випадку полюса порядку  мають місце умови , , нарешті, для істотно особливої точки існує нескінченна множина відмінних від нуля коефіцієнтів головної частини ряду Лорана.

    Лишком функції 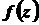 відносно скінченої точки  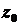називається величина

                       ,

де  – будь-яке додатно орієнтоване коло , яке лежить в кільці збіжності ряду Лорана.

    Якщо точка 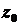 є точкою аналітичності функції  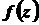або її усувною особливою точкою, то .

    Лишок в простому полюсі обчислюють за формулами

 або

,   де , причому .

    Якщо 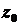 – кратний полюс порядку , то

               .

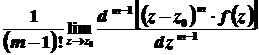    Для обчислення лишків в істотно особливих точках знаходять коефіцієнт  ряду Лорана інтегруванням або за допомогою відомих розвинень функцій у степеневі ряди.

    Основна теорема про лишки. Якщо функція 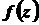  є аналітичною у замкненій області  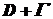за винятком скінченої кількості особливих точок , ,… , які лежать усередині , то

              .

 

Операційне числення

    Операційний метод – це специфічний спосіб розв’язування різних математичних задач, в першу чергу, диференційних рівнянь. Він базується на застосуванні інтегральних перетворень, зокрема, перетворення Лапласа, та складається з таких етапів:

1) від шуканої функції  переходять до функції  комплексної змінної, яку називають зображенням шуканої функції;

2) над зображенням виконують операції, які відповідають заданим операціям над шуканою функцією, – отримують так зване операторне рівняння для зображення ;

3) операторне рівняння розв’язують відносно ;

4) від отриманого зображення  переходять до оригіналу, який є шуканою функцією.