2018-02-20
333
Дифференциальное уравнение теплопроводности в условиях одномерной задачи и без источников теплоты имеет вид
∂ t /∂τ = a ∂2 t /∂ x 2. (3.1)
Это уравнение является частным случаем однородного дифференциального уравнения с постоянными коэффициентами для некоторой функции t от двух переменных x и τ:
(3.2)
Легко проверить, что частным решением этого уравнения будет выражение
t = C exp (α x + βτ). (3.3)
Действительно:
∂ t /∂ x = α С ехр (α x + βτ); ∂ t /∂τ = β С ехр (α x + βτ);
∂2 t /∂ x 2 = α2 С ехр (α x + βτ);
∂2 t /∂τ2 = β2 С ехр (α x + βτ); ∂2 t /(∂ x ∂τ) = αβ С ехр (α x + βτ). (3.4)
Совместное решение последних семи уравнении дает
a 1α2 + b 1αβ + c 1β2 + d 1α + l 1β + f 1 = 0. (3.5)
Последнее уравнение называется уравнением коэффициентов.
Переходя к уравнению (3.1) сопоставляя его с уравнением (3.2), заключаем, что
b 1 = c 1 = d 1 = f 1 = 0; a 1= - a; l 1 = 1. (3.6)
Уравнение коэффициентов (3.5) для частного случая уравнения (3.1) приобретает вид
- α2 a + β = 0 (3.7)
или
β = α2 a. (3.8)
Таким образом, частное решение (3.3) является интегралом дифференциального уравнения (3.1) и с учетом (3.8) приобретет вид
t = C exp (α2 a τ + α x). (3.9)
В этом уравнении можно задавать любые значения чисел для C, α, a.
Выражение (3.9) может быть представлено в виде произведения
t = C exp (α2 a τ) exp (α x), (3.10)
где сомножитель exp (α2 a τ) является функцией только времени τ, а сомножитель exp (α x) — только расстояния x:
exp (α2 a τ) = f (τ); exp (α x) = φ (x). (3.11)
С увеличением времени τ температура во всех точках непрерывно растет и может стать выше наперед заданной, что в практических задачах не встречается. Поэтому обычно берут только такие значения α, при которых α2 отрицательно, что возможно при α чисто мнимой величине.
Примем
α = ± iq, (3.12)
где q — произвольное действительное число (ранее значком q обозначали удельный тепловой поток),
В этом случае уравнение (3.10) приобретет следующий вид:
t = C exp (- q 2 a τ) exp (± iqx). (3.13)
Обращаясь к известной формуле Эйлера
exp (± ix) = cos x ± i sin x (3.14)
и, пользуясь ею, преобразуем уравнение (3.13). Получим два решения в комплексном виде:
(3.15)
Суммируем левые и правые части уравнений (3.15), затем отделим действительные от мнимых частей в левой и правой частях суммы и приравняем их соответственно. Тогда получим два решения:
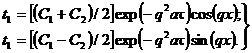(3.16)
Введем обозначения:
(C 1 + C 2)/2 = D; (C 1 - C 2)/2 = C (3.17)
тогда получим два решения, удовлетворяющих дифференциальному уравнению теплопроводности (3.1):
t 1 = D exp (- q 2 a τ) cos (qx); t 2 = C exp (- q 2 a τ) sin (qx). (3.18)
Известно, что если искомая функция имеет два частных решения, то и сумма этих частных решений будет удовлетворять исходному дифференциальному уравнению (3.1), т. е. решением этого уравнения будет
t = C exp (- q 2 a τ) sin (qx) + D exp (- q 2 a τ) cos (qx), (3.19)
а общее решение, удовлетворяющее этому уравнению, можно записать в следующем виде:
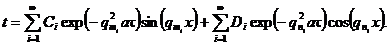(3.20)
Любые значения qm, qn, Ci, Di в уравнении (3.20) будут удовлетворять уравнению (3.1). Конкретизация в выборе этих значений будет определяться начальными и граничными условиями каждой частной практической задачи, причем значения qm и qn определяются из граничных условий, а Ci, и Di, — из начальных.
Помимо общего решения уравнения теплопроводности (3.20) в котором имеет место произведение двух функций, одна из которых зависит от x, а другая - от τ, существуют еще решения, в которых такое разделение невозможно, например:
(3.21)
и
(3.22)
Оба решения удовлетворяют уравнению теплопроводности, в чем легко убедиться, продифференцировав их сначала по τ, а затем 2 раза по x и подставив результат в дифференциальное уравнение (3.1).
