Значения функций, входящих в формулу (3.23)

I	1	2	3	4	5
A=(qniX) 2 (a τ/ X 2)	0,065	0,601	1,723	3,458	5,881
e-A	0,94	0,55	0,18	0,03	0,00
Di e-A	1,175	—0,203	0,033	—0,003	0,000

 

Окончательное выражение для распределения температуры в толще стенки через 5 ч после начального момента

 

(3.26)

 

На рис.3.1 показано распределение температуры в толще стенки на начальный момент времени и через 5 ч. Наряду с общим решением здесь же изображены и частные, причем римскими цифрами указаны частные кривые, отвечающие последовательным слагаемым рядов (3.25) и (3.26).

Рис.3.1. Распределение температуры в стенке на начальный момент времени (слева) и через 5 ч (справа) [8]

 

При решении практических задач обычно нет необходимости определять температуру во всех точках стенки. Можно ограничиться расчетом температуры лишь для какой-либо одной точки, например для точки в середине стенки. В этом случае объем вычислительных работ по формуле (3.23) значительно сократится.

Если начальная температура в рассмотренном выше случае равна не 1 °С, а Т _с, то уравнение (3.20) примет вид

 

(3.27)

 

3.3. Решение уравнения теплопроводности при различных граничных условиях [8]

Не будем приводить последовательный ход решения уравнения теплопроводности при других граничных условиях, которые имеют практическое значение в решении некоторых задач. Ниже ограничимся лишь формулировкой их условий с показом имеющихся готовых решений.

Задача № 1. Исходные данные. Стенка имеет толщину 2 Х. В начальный момент во всех ее точках, кроме поверхности, температура Т _с Температура на поверхности 0°С удерживается в течение всего расчетного периода.

Требуется найти t = f(x, τ).

Решение.

 

 

(3.28)

 

Пример к задаче № 1. Неподвижное водохранилище покрылось льдом при температуре наибольшей плотности воды (Т _с = 4°С). Глубина водохранилища 5м (Х = 5 м). Рассчитать температуру воды в водохранилище через 3 месяца после ледостава. Температуропроводность неподвижной воды a = 4,8·10^-4 м²/ч. Тепловой поток у дна, т. е. при x = 0, отсутствует.

В течение расчетного периода (τ=3·30·24=2160ч) температура на поверхности удерживается постоянной и равной нулю, т. е. при x = Х      Т _п = 0°С.

Весь расчет сводим в табл. 3 и 4. Эти таблицы позволяют вычислить значения температуры через 3 месяца после начального момента для глубин у дна, а затем выше через 1 м, т. е. t _0(дно) = 4°С; t ₁ = 4°С; t ₂ = 3,85°С; t ₃ = 3,30°С; t ₄ = 2,96°С; t _5(пов) = 0°С.

Таблица3.3

Таблица3.4

Как видим, в абсолютно неподвижной воде температурные возмущения весьма медленно проникают вглубь. В природных условиях в водоемах под ледяным покровом всегда наблюдаются течения либо гравитационные (проточные), либо конвективные (разноплотностные), либо, наконец, вызванные поступлением грунтовых вод. Все многообразие указанных природных особенностей следует учитывать при практических расчетах, а рекомендации к этим расчетам можно найти в пособиях и в работах К.И.Россинского [37].

Задача №2. Исходные данные. Тело ограничено с одной стороны (полуплоскость). В момент времени τ = 0 во всех точках температура тела равна Т _с. Для всех моментов времени τ > 0 на поверхности тела поддерживается температура Т _п = 0°С.

Требуется найти распределение температуры в толще тела и потерю теплоты через свободную поверхность как функцию времени: t = f (x, τ),

 

Решение. Температура в любой точке тела и в любой момент времени

 

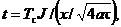(3.29)

 

где есть интеграл Гаусса. Его значения в зависимости от функции 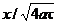 даны в табл.3.5.

Таблица 3.5

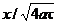Практически решение начинается с определения отношения, в котором х и τ заданы в условии задачи.

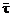Количество теплоты, теряемой единицей поверхности тела в окружающую среду, определяется по закону Фурье. За весь расчетный период с начального момента до расчетного

 

(3.30)

 

Пример к задаче № 2. В начальный момент времени температура почвы от поверхности до значительной глубины была постоянной и равной 6°С. В этот момент температура на поверхности почвы упала до 0°С.

Требуется определить температуру почвы на глубине 0,5 м через 48 ч при значении коэффициента температуропроводности почвы a = 0,001 м²/ч, а также оценить количество теплоты, теряемое поверхностью за это время.

Решение. Определяем значение функции

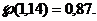Из табл.3.5 находим по интерполяции значение интеграла Гаусса

По формуле (3.29) температура почвы на глубине 0,5 м через 48 ч t =6·0,87=5,2°С.

Общее же количество теплоты, потерянной единицей поверхности почвы, при коэффициенте теплопроводности λ = 0,35 Вт/(м·°С), удельной теплоемкости c = 0,83·10³ Дж/(кг·°С) и плотности ρ = 1500 кг/м³ определим по формуле (3.30) Q =l,86·10⁶ Дж/м².

Рис.3.2 Распределение температуры по глубине толщи [8]

Задача № 3. Исходные данные. Вследствие некоторого внешнего воздействия температура поверхности тела, ограниченного с одной стороны (полуплоскость), претерпевает периодические колебания около нуля. Будем считать, что эти колебания гармонические, т. е. температура поверхности меняется по косинусоиде:

 

(3.31)

 

где t — продолжительность колебания (период), T ₀ — температура поверхности,

T _{0 макс} — ее максимальное отклонение,.

Требуется определить температурное поле как функцию времени.

Решение.

 

(3.32)

 

Амплитуда колебаний температуры меняется с x по следующему закону (рис.3.2):

 

(3.33)

 

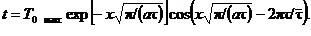Пример к задаче № 3. Изменение температуры на поверхности сухой песчаной почвы в течение года характеризуется косинусоидальным ходом. Средняя годовая температура при этом равна 6°С при максимальных отклонениях от средней летом и зимой, достигающих 24 °С.

Требуется определить температуру грунта на глубине 1 м в момент, когда температура на поверхности равна 30°С (условно 1/VII).

Решение. Выражение косинусоиды (3.31) применительно к данному случаю (температуре поверхности) при T _{0 макс} = 24⁰С примет вид

Т ₀ = 24 cos (2πτ/8760) + 6.

Ввиду того, что поверхность грунта имеет среднюю годовую температуру 6°С, а не нуль, как в уравнении (3.32), расчетное уравнение примет следующий вид:

 

(3.34)

 

Приняв для грунта коэффициент температуропроводности a = 0,001 м²/ч и имея в виду, что по условию задачи необходимо определить температуру на конец расчетного периода (через 8760 ч от начального момента), найдем

 

 

Расчетное выражение (3.34) приобретет следующий вид: t = 24 e ^-0,6·0,825 + 6 = 16,9 °С.

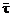На той же глубине 1м максимальная амплитуда годового колебания температуры, согласно выражению (3.33), составит

T _{1 макс} = 24 e ^-0,6 = 13,2 °С,

а максимальная температура на глубине 1 м

t _{1 макс} = T_{x макс} + 6 = 13,2 + 6 =19, 2 °С.

В заключение отметим, что рассмотренные задачи и подходы могут быть использованы при решении вопросов, связанных с выпуском теплой воды в водоем, а также при химическом методе определения расхода воды и в других случаях.

 

4. РАСЧЕТ ТЕПЛОВЫХ ПОТОКОВ ЧЕРЕЗ ПОВЕРХНОСТЬ И ДНО ВОДОЕМА

Сумма тепловых потоков, проходящих через поверхности водоема и определяющих его тепловой баланс, может быть представлена в следующем виде:

 

(4.1)

 

где Q_R — количество теплоты, определяемое радиационным балансом водной поверхности; Q _к — количество теплоты, обусловленное конвективным теплообменом между водной поверхностью и воздушной средой над водоемом; Q _и — количество теплоты (теплоотдача), определяемое испарением воды с поверхности водоема (или количество теплоты, приходящее при конденсации пара); Δ Q _пр — количество теплоты, приносимое водами притоков или промышленными водами; Q _д — количество теплоты, обусловленное теплообменом между водой и дном; Δ Q _гр — количество теплоты, приносимое грунтовыми водами; Δ Q _ос — теплота, поступающая в водоем с осадками.

Другие элементы теплового баланса в уравнении (4.1) за их малостью не рассматриваются. Например, для рассматриваемых водоемов не учитывается теплота перехода механической энергии движения воды в тепловую энергию, теплота биохимических процессов и ряд других несущественных составляющих теплового баланса, значения которых лежат в пределах точности расчетов.

В уравнении (4.1) величина Q_R всегда по знаку положительная, а остальные элементы могут иметь разные знаки.

Дифференциальное уравнение (в лекционном курсе (5.19)) позволяет

 

(*)

 

определить ход во времени средней по глубине температуры воды при заданных значениях составляющих правой части уравнения. Рассмотрим составляющие теплового баланса и методы их расчета для открытых водоемов. Все составляющие измеряются в ваттах на квадратный метр.

1. Радиационный баланс. Количество теплоты, равное поглощенной водой солнечной радиации за вычетом эффективного излучения определяется по формуле (в лекционном курсе (3.21в)):

Q_R = (1 - A) (Q _п.р + q _р.р) – I _эф.                       (4.2)

Правая часть равенства (4.2) включает в себя суммарную солнечную радиацию Q _п.р + q _р.р при наличии облачности, падающую на водную поверхность, и эффективное излучение воды I _эф. Суммарная солнечная радиация состоит из прямой (Q _п.р) и рассеянной (q _р.р) радиации. Интенсивность ее меняется с высотой Солнца, высотой местности над уровнем моря, а также зависит от прозрачности атмосферы, облачности и других факторов. При отсутствии данных актинометрических наблюдений суммарная солнечная радиация может быть рассчитана по формулам в зависимости от интенсивности солнечной радиации при безоблачном небе (Q _п.р + q _р.р)₀. Интенсивность солнечной радиации при безоблачном небе для любой точки земного шара и любого часа года оценивается по формулам (например, по формуле М.Е.Берлянда) и таблицам [36].

Поступившая к поверхности воды солнечная радиация только частично ею поглощается, другая часть отражается водной поверхностью. Отраженная радиация зависит от альбедо этой поверхности A (в лекционном курсе Лекция №4-5). При большой высоте Солнца альбедо имеет минимальное значение, при приближении же Солнца к горизонту оно увеличивается в несколько раз. Значения альбедо водной поверхности можно найти в таблице [36], составленной для различных широт земного шара.

Поверхность воды излучает теплоту в окружающее ее пространство. В свою очередь, от атмосферы приходит встречный поток излучения к воде, основную роль в котором играет водяной пар. Разность теплоты этих потоков является эффективным излучением водной поверхности. Эффективное излучение при безоблачном небе может быть оценено по таблице [36].

Из большого числа формул, принятых для расчета радиационного баланса, рассмотрим только те, которые приводятся в рекомендациях [36]:

формула А.П.Браславского и З.А.Викулиной

 

(4.3)

 

формула М.И.Будыко

 

(4.4)

 

В этих формулах (Q _п.р + q _р.р)₀ — суммарная солнечная радиация при безоблачном небе на уровне моря; А — альбедо поверхности воды в относительных единицах; k_е, k_z, k _н, k _в+с, k, c — коэффициенты, зависящие от влажности воздуха, высоты местности над уровнем моря, облачности нижнего и совместно верхнего и среднего ярусов, географической широты и других факторов; п ₀, п _н — облачность общая и нижняя в долях единицы; γ — доля радиации, повторно рассеянной облаками по направлению к поверхности воды; σ — постоянная Стефана—Больцмана; Т _п и Т _θ — абсолютная температура поверхности воды и воздуха на высоте 2 м; b ₁ и b ₂ — величины, зависящие от влажности воздуха и облачности; I эф₀ — эффективное излучение при безоблачном небе.

2. Конвективный теплообмен. Теплоотдача испарением. Рекомендации по расчету количества теплоты, определяемой конвективным теплообменом (Q _к) и испарением (Q _и) здесь рассматривать не будем, так как они приведены в лекционном курсе (Лекция №4-5) при рассмотрении основных закономерностей температурного поля.

3. Количество теплоты, приносимое водами притоков или промышленными водами, отнесенное к единице его поверхности, определяется по формуле

Δ Q _пр = [(c ρ Q _в)/Ω] Δ t,                                     (4.5)

где Q _в — средний за период расчета расход воды притока; Ω — площадь водной поверхности водоема; Δ t = t _пр - t _в — разность между температурой воды приток а и водоема.

4. Теплообмен с дном. Теплообмен между водой и грунтом дна оценивается в зависимости от типа водоема. В том случае, когда водоем мелкий (неглубокий) оценка количества теплоты, проходящей через дно, осуществляется по закону Фурье (формула (3.9) в лекционном курсе Лекция №4-5):

(4.6)

 

В глубоком водоеме градиент температуры принимается равным нулю, а в очень глубоком - температура предполагается постоянной у дна, т. е. и

Поэтому в таких водоемах теплообмен с дном равен нулю.

Для определения теплообмена с дном по формуле (4.6) необходимы данные о ходе придонной температуры воды или о ходе температуры грунта, слагающего дно. Эти сведения получить весьма трудно: необходимо выполнить натурные измерения либо задать ход температуры со стороны воды или со стороны грунта. Оба пути неприемлемы в случае вычисления температуры воды водоема или расчета его теплового баланса. Поэтому рекомендуется пользоваться готовой таблицей [36] для определения средних значений потоков теплоты через дно водоема, составленной для различных широт территории бывшего СССР и различных месяцев года.

5. Количество теплоты, приносимое грунтовыми водами, обусловливающее изменение энтальпии водоема, отнесенное к единице его поверхности, определяется по формуле

Δ Q _гр = [(c ρ Q _гр)/Ω] Δ t,                                    (4.7)

где Q _гр — средний за период расчета расход грунтовой воды; Δ t = t _гр - t _в — разница между температурой грунтовой воды и водоема.

6. Приход теплоты с атмосферными осадками. Количество теплоты, поступающее в водоем с атмосферными осадками, определяется по одной из следующих формул:

для жидких осадков

Q _ос.ж = c ρ h _жθ_2,ж ,                                            (4.8)

для твердых осадков

Q _ос.т = -(c _тρ_т h _тθ_2,т + L _плρ_т h _т + c ρ h _т,ж t),           (4.9)

где h _ж и h _т — слой жидких и твердых осадков; θ_2,ж и θ_2,т — температура жидких и твердых осадков, принимаемая равной температуре воздуха на высоте 2 м; c _т и ρ_т — удельная теплоемкость и плотность твердых осадков; h _т,ж — слой жидких осадков, образовавшийся из твердых; t — температура воды водоема; L _пл — удельная теплота плавления твердых осадков.

В формуле (4.9) первое слагаемое справа учитывает количество теплоты, необходимое для нагревания твердых осадков от температуры θ_2,т до 0°С, второе — количество теплоты, необходимое для расплавления твердых осадков, третье — количество теплоты, необходимое для нагревания жидких осадков, полученных от таяния твердых, от температуры 0°С до температуры водоема t.