Интиеграл от ф-и комплексной переменной. Сведения к вычислению обыкновенного интеграла

Пусть L- гладкая кривая комплексной плоскости. Зададим кривую L уравнением в параметрическом виде: z=l(t)=x(t)+i[y(t)], a£t£b, начало z₀=l(t), z’=l(b)-конец (если направление от a до b. Изменим направление кривой L и обозначим L’. выберем монотонныю последовательность n+1 в значении t. t0,t1,t2,..,tn. Этому выбору соответствует разбиение Т кривой L на n дуг (l_i). Выберем дугу l_i. Рассмотрим f(z)=U(x,y)+iV(x,y) - непрерывна на L. Рассмотрим комплексную интегральную сумму разбиения Т:  , рассм значение ф-и  ;z_i+1-z_i=Δz_i= Δxi+iΔy_i.

Определение интеграла от Ф.К.П.: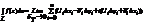

Пусть L- гладкая кривая, l(t)=x(t)+i[y(t)], a£t£b, н ф-я l(t) имеет непрерывные производные на этом отрезке: l’(t)=x’(t)+i[y’(t)]. Геометрическая гладкость кривой означает, что в каждой точке этой кривой сущ касательная кривой, причем угол наклона касательной к действительной оси непрерывно меняются при движении точки по кривой.   

_a∫^bf(l(t))*l’(t))dx= _L∫f(z)dz.

Теор: если ф-я а(я)однозначна и аналитична в односвязной обл G для любой замкнутой кусочно-гладкой кривой L содержащейся в G:

Область G назыв односвязной, если для любой замкнутой кусочно-гладкой кривой g<G, внутренность g<G.

Интегральная теор Коши. Теорема о составном контуре.

Теор: пусть f(z) – однозначна и аналитична в многосвязной области D на её границе, которая представляет совокупность замкнутых кус-гладких контуров g1,g2,…gn, причем все gi находятся во внутренности области D, g и любая gi-граница области D=>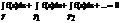

Опр: положительной ориентацией границы области D, назовем такую ориентацию, составляющие её контуров g1,g2,…gn, что при полном обходе любого контура внутренность обл D остается слева от обходящего.

Интегральная теор Коши: если ф-я f(z) аналитична в D и на её границе, составной контур Г, ориентирован положительно, то