Разложение аналитической ф-и в ряд Тейлора. Ряд Лорана. Теорема Лорана

Если ф-я f(z) – однозначна и аналитична в области G, т. z₀ÎG, к – расстояние от z₀ до границы обл G, то в круге |z-z₀|<r ф-ю f(z) можно разложить в ряд Тейлора по степеням

(z-z₀).

Рядом, обобщающий понятия ряда по целым неотрицательным степеням (z-z₀) или по целым неположительным степеням (z-z₀) явл-ся ряд Лорана:

Ряд (1) сходится, если сходятся (1)и (2). Ряд (1) сходится абсолютно и равномерно во внутренности круга |z-z₀|=R и расходится вне её. Если ряд r<R, то ряд (3) сходится абсол и равномерно в круговом кольце r<|z-z₀|<R.

Если рассмотреть r, которое находится м/у r и R, то ряд (3) равномерно сходится на окружности g_r:|z-z₀|=r, он будет сход на данной окружности и после того, как все члены ряда (3) умножить на [1/2Пi]*(z-z₀)^-k-1.

После интегрирования обеех частей по я имеем: - ф-ла для определения коэффициента ряда Лорана.

Теор Лорана: если f(z) однозначна и аналитична в круговом кольце r<|z-z₀|<R, то в этом кольце её можно разложить в ряд Лорана.

Нули аналитической функции.

Пусть f(z) – аналитична в т. z₀=> f(z) – аналитич в некот окрестности т. z₀ => f(z) можно разложить в ряд Тейлора по степеням z-z₀.

Если f(z)¹0, то сущ целое неотрицательное k принадлежащее z, f^(k)(z₀)¹0, f^(m)(z₀)¹0, m<k

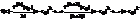
Тогда f(z)=(z-z₀)^kj(z₀), где j(z₀) – аналитична в окрестности т. z₀, j(z₀)¹0. Число k назыв кратностью или порядком ф-и f(z) в т. z₀.

Если k=1, т. z₀ назыв простым нулем ф-и f(z) [f(z₀)=0; f’(z₀)¹0].

Если k>1, т. z₀ кратный нуль f(z) [f(z₀)=0; f’(z₀)= 0; f^(k-1)(z₀)¹0 => т. z₀ – нуль порядка k].