Вероятностное пространство  называется дискретным, если
называется дискретным, если 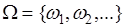 конечно или счетно,
конечно или счетно,  -
-  - алгебра всех подмножеств
- алгебра всех подмножеств 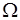 (включая
(включая 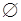 ), вероятность
), вероятность  определена для каждого одноточечного подмножества
определена для каждого одноточечного подмножества  пространства элементарных событий
пространства элементарных событий  :
:
 ,
,  , (16.1)
, (16.1)
 . (16.2)
. (16.2)
Для любого события 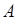 его вероятность
его вероятность 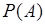 определяется равенством
определяется равенством
 . (16.3)
. (16.3)
Примеры 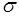 - алгебр
- алгебр
17.1. Пусть  - произвольное пространство элементарных событий, на котором не заданы какие-либо события. Для построения
- произвольное пространство элементарных событий, на котором не заданы какие-либо события. Для построения 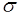 - алгебры согласно определению (п.15) необходимо рассмотреть все дополнения, объединения и пересечения заданных событий и включить их в
- алгебры согласно определению (п.15) необходимо рассмотреть все дополнения, объединения и пересечения заданных событий и включить их в 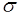 - алгебру. Поскольку в данном случае имеется единственное событие
- алгебру. Поскольку в данном случае имеется единственное событие 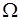 , то возможно построить только его дополнение
, то возможно построить только его дополнение  . Теперь имеется система из двух событий {
. Теперь имеется система из двух событий {  }. Дальнейшее применение операций дополнения, объединения, пересечения не дает новых событий. Таким образом, в данном примере
}. Дальнейшее применение операций дополнения, объединения, пересечения не дает новых событий. Таким образом, в данном примере 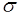 - алгебра
- алгебра 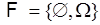 .
.
17.2. Пусть  - пространство элементарных событий и
- пространство элементарных событий и  - некоторое событие, не совпадающее с
- некоторое событие, не совпадающее с 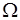 , т.е.
, т.е.  . Таким образом, имеется система из двух событий
. Таким образом, имеется система из двух событий  . Эту систему можно расширять, включая в нее новые события, которые получаются в результате операций дополнения, объединения, пересечения над событиями
. Эту систему можно расширять, включая в нее новые события, которые получаются в результате операций дополнения, объединения, пересечения над событиями 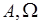 . Процедуру расширения системы событий имеет смысл продолжить рекуррентно до прекращения появление новых событий. Предельная система событий называется
. Процедуру расширения системы событий имеет смысл продолжить рекуррентно до прекращения появление новых событий. Предельная система событий называется  - алгеброй, порожденной системой событий
- алгеброй, порожденной системой событий 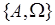 .
.
Рассмотрим операцию дополнения над событиями системы. Ее результат 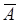 ,
,  - это новые события, не содержащиеся в исходной системе
- это новые события, не содержащиеся в исходной системе 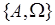 , включение которых дает новую систему событий
, включение которых дает новую систему событий
 . (17.1)
. (17.1)
Очевидно, последующие операции дополнения, объединения, пересечения не дают новых событий, не содержащихся в (17.1). Таким образом, система событий (17.1) является 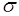 - алгеброй, порожденной системой
- алгеброй, порожденной системой  .
.
17.3. Усложним пример. Пусть 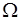 - пространство элементарных событий,
- пространство элементарных событий,  - два несовместных события, таких что
- два несовместных события, таких что 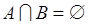 . Таким образом, имеется система трех событий
. Таким образом, имеется система трех событий 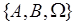 . Операция объединения над событиями этой системы приводит к появлению одного нового события
. Операция объединения над событиями этой системы приводит к появлению одного нового события 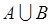 . Полученная система четырех событий расширяется до восьми путем включения их дополнений. Несложно видеть, что применение операций дополнения, объединения, пересечения к этим восьми событиям не порождает новых событий. Таким образом, система восьми событий
. Полученная система четырех событий расширяется до восьми путем включения их дополнений. Несложно видеть, что применение операций дополнения, объединения, пересечения к этим восьми событиям не порождает новых событий. Таким образом, система восьми событий
 (17.2)
(17.2)
является  - алгеброй, порожденной системой событий
- алгеброй, порожденной системой событий 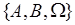 .
.
17.4. Рассмотрим 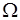 - пространство элементарных событий и два произвольных события
- пространство элементарных событий и два произвольных события  , рис. 17.1. Для построения
, рис. 17.1. Для построения 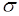 - алгебры, порожденной некоторой системой событий, во многих случаях удобно применить следующий прием.
- алгебры, порожденной некоторой системой событий, во многих случаях удобно применить следующий прием.
На  выделим все несовместные события
выделим все несовместные события 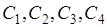 , рис. 17.1. При этом
, рис. 17.1. При этом  ,
,  ,
,  ,
, 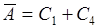 ,
, 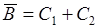 и т.д.
и т.д. 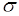 - алгебра будет содержать все события
- алгебра будет содержать все события  , все объединения событий
, все объединения событий  , а также невозможное событие
, а также невозможное событие  . Действительно, операция пересечения любых событий из множества
. Действительно, операция пересечения любых событий из множества 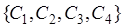 порождает единственное событие
порождает единственное событие  . Операция дополнения над событиями из множества
. Операция дополнения над событиями из множества 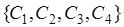 порождает событие, которое выражается через объединение событий
порождает событие, которое выражается через объединение событий 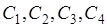 . Следовательно, над событиями
. Следовательно, над событиями 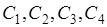 достаточно рассмотреть только операцию объединения, вместо трех операций - дополнения, пересечения, объединения для исходной системы событий
достаточно рассмотреть только операцию объединения, вместо трех операций - дополнения, пересечения, объединения для исходной системы событий  .
.
Теперь для построения 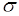 - алгебры рассмотрим события
- алгебры рассмотрим события  , все их объединения и выразим полученные события через исходные
, все их объединения и выразим полученные события через исходные  . Очевидно:
. Очевидно: 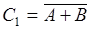 ,
,  ,
, 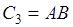 ,
, 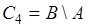 . Парные объединения дают следующие события:
. Парные объединения дают следующие события: 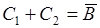 ,
, 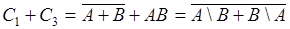 ,
, 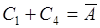 ;
;  ,
, 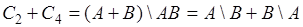 ;
;  . Тройные объединения:
. Тройные объединения:  ,
, 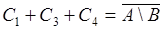 ,
, 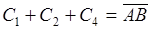 ,
, 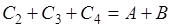 .
.
Таким образом, 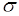 - алгебра содержит события:
- алгебра содержит события: 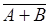 ,
,  ,
, 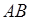 ,
,  ;
;  ,
,  ,
,  ,
, 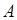 ,
,  ,
,  ;
; 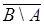 ,
,  ,
, 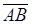 ,
, 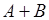 , а также
, а также 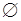 и
и 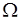 - всего 16 событий.
- всего 16 событий.
Отметим, что при определении 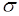 - алгебры порождающая система событий, как правило, составляется из событий, наблюдаемых в опыте.
- алгебры порождающая система событий, как правило, составляется из событий, наблюдаемых в опыте.
Отметим, что события 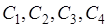 совпадают с событиями (8.1), которые рассматривались при выводе формулы сложения для частот. Действительно,
совпадают с событиями (8.1), которые рассматривались при выводе формулы сложения для частот. Действительно,  ,
,  ,
, 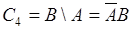 и наконец, по формуле (6.1)
и наконец, по формуле (6.1) 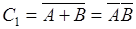 .
.
17.5. Рассмотрим обобщение примера 4. Пусть исходная система событий 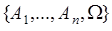 - содержит
- содержит 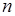 произвольных событий
произвольных событий  . Для построения
. Для построения 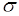 - алгебры, подобно примеру 4, введем события вида
- алгебры, подобно примеру 4, введем события вида
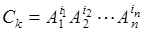 , (17.3)
, (17.3)
где каждое 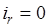 или
или 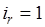 , причем
, причем 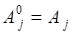 и
и 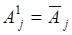 . Поскольку каждое
. Поскольку каждое 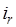 может принимать два значения 0 или 1, то число всех событий вида
может принимать два значения 0 или 1, то число всех событий вида 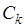 равно
равно  . Эти события образуют полную группу несовместных событий. Таким образом, события
. Эти события образуют полную группу несовместных событий. Таким образом, события 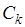 на
на 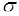 - алгебре выполняют роль ортогонального базиса, позволяющего представить произвольное событие
- алгебре выполняют роль ортогонального базиса, позволяющего представить произвольное событие 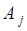 через несовместные (ортогональные в смысле операции пересечения) события
через несовместные (ортогональные в смысле операции пересечения) события  . В теории множеств множества вида
. В теории множеств множества вида 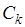 называются конституентами. Аппарат конституент позволяет показать, что в данном примере число всех событий
называются конституентами. Аппарат конституент позволяет показать, что в данном примере число всех событий 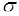 - алгебры не превышает
- алгебры не превышает 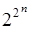 (включая
(включая 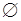 и
и  ), причем число событий достигает максимального значения, когда все
), причем число событий достигает максимального значения, когда все 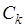 отличны от
отличны от 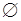 (как в примере 4). Этот результат позволяет судить о высокой скорости роста числа событий в
(как в примере 4). Этот результат позволяет судить о высокой скорости роста числа событий в 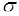 - алгебре в зависимости от
- алгебре в зависимости от  - числа событий в исходной системе. Для примера 4 число
- числа событий в исходной системе. Для примера 4 число  , следовательно, число событий в
, следовательно, число событий в 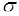 - алгебре равно
- алгебре равно 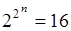 .
.
 2020-01-15
2020-01-15 470
470








