Условная вероятность и вероятностное пространство

18.1. Пусть  - вероятностное пространство. Рассмотрим интерпретацию условной вероятности  события 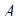, если известно, что произошло событие , причем 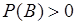. При этих условиях пространством элементарных событий естественно считать не , а 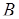, поскольку тот факт, что  произошло, означает, что речь идет лишь о тех элементарных событиях 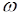, которые принадлежат множеству . Среди элементарных событий , только те из них влекут событие 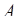, которые принадлежат . 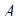Поскольку событие  отождествляется с множеством элементарных событий, влекущих 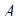, то теперь (при условии, что  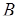- произошло) событие  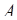следует отождествлять с множеством 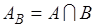. Можно сказать, что множество  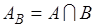есть событие , рассматриваемое с точки зрения, согласно которой пространством элементарных событий объявлено событие .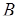

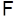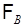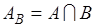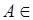
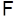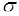18.2. На новом пространстве элементарных событий   - алгебра событий  определяется, или, как говорят, индуцируется - алгеброй событий , а именно  состоит из событий вида , где . Проверим, что  действительно - алгебра. Пусть - события из , где 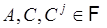. Необходимо показать, что их объединения, пересечения и дополнения также принадлежат .

Рассмотрим объединение

    .                                (18.1)

Операции объединения и пересечения взаимно дистрибутивны, в частности, пересечение дистрибутивно относительно объединения:

    ,                       (18.2)

где 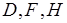 - события. Пусть , , 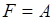, тогда из (18.1) следует

    .                       (18.3)

Поскольку , , 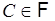а - - алгебра, то и объединения 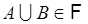. Поэтому 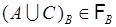, а согласно (18.3) 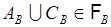. Аналогично

    .     (18.4)

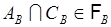Следовательно, . Проверить факт  не составляет труда, действительно,

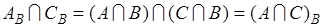    .              (18.5)

Наконец, рассмотрим дополнение

    ,            (18.6)

откуда следует 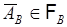. Таким образом,  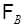является - алгеброй событий вида .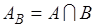

18.3. На - алгебре 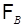 вводится вероятность

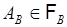    , .                               (18.7)

Отметим, что если положить , то 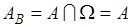, , 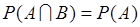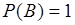. Поэтому в (18.7) знаменатель  выполняет нормировку на новое пространство элементарных событий .

Теперь тройка  является новым вероятностным пространством, построенным в связи с поставленной задачей, в которой событие 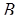 обычно рассматривается как результат опыта. Причем вероятность  на  (18.7) можно рассматривать и на , при этом 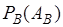 также является вероятностью и обозначается 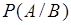. Поэтому (18.7) можно представить:

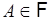    , .                                (18.8)

Вероятность 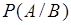 как функция на  называется условной вероятностью события 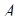 при условии, что событие  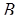произошло.

18.4. Отметим, что свойства условной вероятности аналогичны соответствующим свойствам безусловной вероятности. В частности, имеют место соотношения:

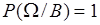    ,                                        (18.9)  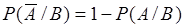  ,                       (18.10)

Для несовместных событий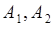

    ,        (18.11)

    ,           (18.12)

где событие под знаком вероятности можно преобразовать: 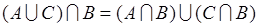. Поэтому в (18.12)

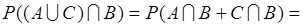
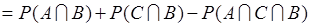    .                 (18.13)

Подставим (18.13) в (18.12), тогда

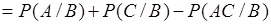    .               (18.14)

Это соотношение полностью аналогично формуле сложения безусловных вероятностей.