Гипергеометрическое распределение

Пусть дана совокупность объектов, среди которых отмеченных (например, бракованных изделий, белых шаров, выигрышных билетов и т.п.). Извлекается наугад объектов. Определить вероятность того, что среди них окажется отмеченных.

Постановка задачи требует уточнения. Можно рассматривать два следующих варианта дополнительных условий. 1). Извлечение с возвращением. При этом извлечение каждого объекта - это отдельный опыт, после которого объект возвращается в исходную совокупность с последующим перемешиванием всех объектов. Таким образом, задача укладывается в вероятностную схему Бернули с вероятностью успеха в одном опыте и числом опытов . Вероятность можно вычислить по формуле Бернули. 2). Извлечение без возвращения. Этот вариант приводит к новой задаче. Рассмотрим ее решение.

Поскольку порядок расположения извлекаемых объектов не имеет значения, то число способов выбора объектов из совокупности различных объектов равно

, (24.1)

и представляет собой общее число возможных исходов опыта. Из отмеченных объектов можно выбрать объектов 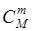способами, причем каждому такому способу соответствует способов добрать еще объектов до общего числа , выбирая их из неотмеченных. Следовательно, число способов, благоприятствующих появлению отмеченных объектов среди выбранных, равно . Поэтому

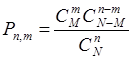. (24.2)

Формула (24.2) называется гипергеометрическим распределением вероятностей.

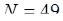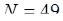Рассмотрим пример вычисления вероятностей выигрыша в игре «спортлото». В данном случае (число номеров на карточке), - число выигрышных номеров (т.е. отмеченных). По условию игрок выбирает номеров из номеров. При этом игрок может угадать выигрышных номеров, .

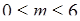Вероятность этого события 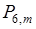можно вычислить по формуле (24.2). При 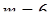получим вероятность максимального выигрыша

Отметим, что результат в виде произведения чисел 6/49,..., 1/44 может быть получен из формулы умножения вероятностей.

Асимптотика Пуассона

25.1. Формула Бернули приводит при больших к очень громоздким вычислениям. Поэтому важное значение имеют приближенные, но более простые формулы, которые можно получить из биномиального распределения. Часто встречаются задачи, в которых рассматривается большое число независимых опытов, причем вероятность успеха в каждом отдельном опыте мала. В этом случае вероятности того, что в серии из опытов число успешных опытов будет равно могут быть вычислены по формуле Пуассона, которая получается как асимптотика биномиального распределения, при условии, что число опытов , а вероятность успеха в отдельном опыте , так что параметр

. (25.1)

Рассмотрим вывод формулы Пуассона. Из (25.1) выразим и подставим в формулу Бернули, тогда

. (25.2)

При наивероятнейшее число распределения Бернули равно , а согласно (25.1) . Это означает, что имеет существенные значения только при , а с увеличением вероятность . Поэтому, полагая в (25.2) , получаем

. (25.3)

Разложим в ряд Тейлора функцию при малом :

. (25.4)

Используем эту формулу для преобразования выражения

. (25.5)

Оставляя здесь только первое слагаемое, получим

. (25.6)

Аналогично рассмотрим

. (25.7)

Подставим (25.6), (25.7) в формулу (25.3), тогда

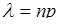, , . (25.8)

Это равенство называется асимптотической формулой Пуассона или распределением Пуассона.

Отметим, что асимптотику (25.8) можно рассматривать в пределе при и , где не зависит от 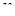. Тогда

, . (25.9)

Распределение вероятностей (25.9) удовлетворяет условию

. (25.10)

25.2. Определим наивероятнейшее число 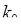распределения Пуассона (25.9). Очевидно число удовлетворяет двум условиям:

, . (25.11)

Подставим формулу (25.9) в первое неравенство, тогда

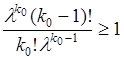. (25.12)

Отсюда следует 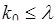. Аналогично решение второго неравенства сводится к условию . Таким образом, наивероятнейшее число 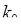распределения Пуассона определяется условием: