21.1. Пусть эксперимент  может быть повторен
может быть повторен  раз. Тогда говорят о последовательности (или серии) испытаний (опытов, экспериментов). Пусть последовательность опытов характеризуется тем, что результат любого опыта не зависит от результатов остальных опытов данной последовательности. Тогда говорят о последовательности независимых испытаний. Пусть опыт
раз. Тогда говорят о последовательности (или серии) испытаний (опытов, экспериментов). Пусть последовательность опытов характеризуется тем, что результат любого опыта не зависит от результатов остальных опытов данной последовательности. Тогда говорят о последовательности независимых испытаний. Пусть опыт  имеет два исхода - событие
имеет два исхода - событие  или
или 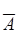 . Тогда последовательность независимых испытаний называется вероятностной схемой Бернулли. Обычно исход
. Тогда последовательность независимых испытаний называется вероятностной схемой Бернулли. Обычно исход 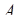 условно называют успехом, а исход
условно называют успехом, а исход  - неудачей. Обозначим вероятность успеха
- неудачей. Обозначим вероятность успеха  и вероятность неудачи
и вероятность неудачи 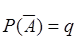 . Очевидно
. Очевидно  .
.
В качестве примеров схемы Бернулли можно привести опыт с бросанием монеты или игральной кости. В первом примере успех 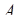 - это выпадение герба и неуспех
- это выпадение герба и неуспех 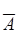 - выпадение решетки, при этом
- выпадение решетки, при этом 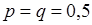 . Во втором примере в качестве успеха
. Во втором примере в качестве успеха  можно рассматривать выпадение грани с номером 1, тогда
можно рассматривать выпадение грани с номером 1, тогда 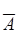 - невыпадение номера 1, при этом
- невыпадение номера 1, при этом 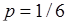 и
и 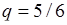 .
.
Определим в схеме Бернулли вероятность 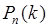 того, что в серии из
того, что в серии из  испытаний успех наступит
испытаний успех наступит 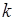 раз. Очевидно
раз. Очевидно 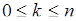 . Рассмотрим последовательность
. Рассмотрим последовательность  опытов и будем фиксировать результат каждого опыта, то есть событие
опытов и будем фиксировать результат каждого опыта, то есть событие 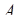 или
или 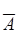 . Тогда последовательность исходов может иметь, например, вид
. Тогда последовательность исходов может иметь, например, вид
 , (21.1)
, (21.1)
то есть ее первые 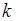 элементов - это события
элементов - это события 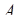 и последующие
и последующие  элементов - события
элементов - события  . Другими словами, в первых
. Другими словами, в первых 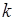 опытах наступает успех и в последующих
опытах наступает успех и в последующих 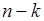 опытах - неуспех. По условию исходы в последовательности (21.1) - это независимые события, поэтому по формуле умножения вероятность
опытах - неуспех. По условию исходы в последовательности (21.1) - это независимые события, поэтому по формуле умножения вероятность 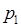 появления последовательности вида (21.1) равна
появления последовательности вида (21.1) равна
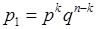 . (21.2)
. (21.2)
При подсчете вероятности 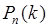 следует учесть все возможные последовательности, состоящие из
следует учесть все возможные последовательности, состоящие из 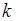 событий
событий 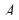 и
и  событий
событий 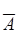 . Вероятность появления любой их этих последовательностей одинакова и равна
. Вероятность появления любой их этих последовательностей одинакова и равна 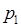 . Кроме этого последовательности являются несовместными событиями, поскольку в каждой серии опытов реализуется только одна из этих последовательностей. Поэтому по формуле сложения вероятностей:
. Кроме этого последовательности являются несовместными событиями, поскольку в каждой серии опытов реализуется только одна из этих последовательностей. Поэтому по формуле сложения вероятностей:
 , (21.3)
, (21.3)
где суммирование ведется по всем последовательностям, содержащим 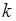 событий вида
событий вида 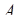 и
и  событий
событий 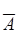 . Число этих последовательностей равно
. Число этих последовательностей равно 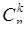 , поскольку может быть определено как число различных перестановок элементов последовательности (21.1), содержащей
, поскольку может быть определено как число различных перестановок элементов последовательности (21.1), содержащей 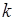 элементов 1-го типа (событий
элементов 1-го типа (событий 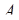 ) и
) и  элементов 2-го типа (событий
элементов 2-го типа (событий 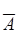 ) по формуле (19.6). Таким образом, из (21.3) следует
) по формуле (19.6). Таким образом, из (21.3) следует
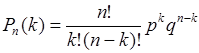 . (21.4)
. (21.4)
Это соотношение называется формулой Бернулли или биномиальным распределением вероятностей. Последнее связано с тем, что 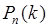 равно общему члену бинома
равно общему члену бинома  .
.
Рассмотрим пример. Бросается монета. Какова вероятность выпадения 0,1,2,3,4 раз герба при 4 бросаниях? Здесь вероятность успеха (появления герба) в одном опыте равна 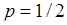 ,
, 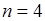 ,
,  По формуле (21.4) вычисляются вероятности
По формуле (21.4) вычисляются вероятности  ,
, 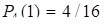 ,
, 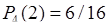 ,
, 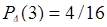 ,
, 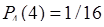 . На рис. 21.1 представлен график зависимости
. На рис. 21.1 представлен график зависимости 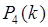 .
.
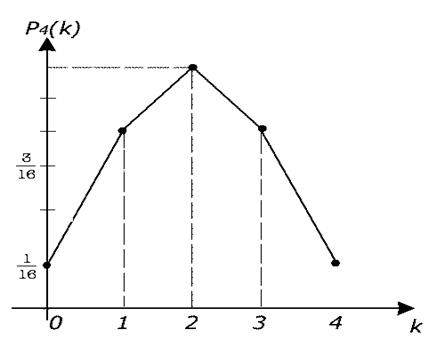
Рис. 21.1. График зависимости вероятности от числа успехов в опыте с бросанием монеты.
21.2. Вычислим вероятность 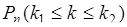 того, что в серии из
того, что в серии из  независимых опытов число успехов
независимых опытов число успехов 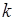 будет лежать в интервале
будет лежать в интервале 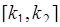 . В соответствии с формулой сложения вероятностей
. В соответствии с формулой сложения вероятностей
 . (21.5)
. (21.5)
Определим, какова вероятность появления хотя бы одного успеха в серии из  опытов. Очевидно, речь идет о вероятности того, что число успехов
опытов. Очевидно, речь идет о вероятности того, что число успехов 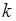 будет лежать в интервале
будет лежать в интервале  . Таким образом, искомая вероятность определится формулой (21.5) при
. Таким образом, искомая вероятность определится формулой (21.5) при 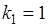 и
и  :
:
 . (21.6)
. (21.6)
Это выражение можно преобразовать, если учесть равенство
 . (21.7)
. (21.7)
Левая часть (21.7) согласно формуле сложения вероятностей представляет собой вероятность события, состоящего в том, что число успехов 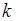 принимает значение из интервала
принимает значение из интервала 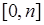 . Это событие является достоверным, поэтому его вероятность равна единице. Теперь (21.6) можно представить в виде:
. Это событие является достоверным, поэтому его вероятность равна единице. Теперь (21.6) можно представить в виде:
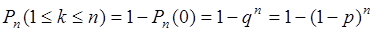 . (21.8)
. (21.8)
 2020-01-15
2020-01-15 127
127








