Интегральная теорема Муавра-Лапласа

Вероятность  того, что в последовательности  независимых испытаний число 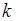 успехов находится в интервале определяется выражением

.                           (28.1)

Получим асимптотику выражения (28.1) при тех же условиях, которые были определены для локальной теоремы Муавра-Лапласа. При этом  определяется формулой (27.18). Подставим (27.18) в (28.1), тогда

        (28.2)

где

.                      (28.3)

Поскольку , то  при . Пусть

, .                    (28.4)

Тогда при  сумма в выражении (28.2) переходит в интеграл:

.              (28.5)

Этот результат носит название интегральная теорема Муавра-Лапласа. Соотношение (28.5) можно представить через функцию Лапласа:

.                         (28.6)

Практическое применение интегральной теоремы основано на приближенном равенстве:

.                                (28.7)

Для функции  составлены подробные таблицы, которые обычно используются при решении задач. Вместо функции Лапласа (28.6) может быть использован интеграл ошибок:

.                           (28.8)

Функции  и  связаны соотношением:

 .

Если в таблицах даны значения  только для  , тогда значения  при  можно вычислить, используя очевидное равенство

 .

Рассмотрим примеры вычисления вероятностей с использованием теоремы Муавра-Лапласа.

1. Какова вероятность того, что при 200 бросаниях монеты герб выпадет 100 раз?

Для вычисления вероятности можно использовать локальную асимптотику (27.18). Здесь , , , , . Поскольку , то . Подставим полученные результаты в (27.18), тогда:

.                                 

2. Какова вероятность того, что при 200 бросаниях герб выпадет в интервале от 80 до 120 раз?

Решать эту задачу удобно, используя интегральную асимптотику из (28.7). Здесь , , , . Необходимо найти . Определим по формулам (28.4)

,                                 

 .                                    

Теперь по (28.7): .