Конспект лекции: Эконометрика как наука расположена где-то между экономикой, статистикой и математикой. Эконометрика – это наука, связанная с эмпирическим выводом экономических законов. То есть мы используем данные или «наблюдения» для того, чтобы получить количественные зависимости для экономических соотношений.
Во всей этой деятельности существенным является использование моделей. Можно выделить три основных класса моделей, которые применяются для анализа и/или прогноза: модели временных рядов; регрессионные модели с одним уравнением; системы одновременных уравнений. Если модель содержит только одну объясняющую переменную, т.е. k=1, она называется парной регрессией. При k>1 мы имеем дело с множественной регрессией.
Основу эконометрического моделирования составляют статистические данные. Их различают по типам. Перекрестные данные собираются по какому-либо экономическому показателю для разных объектов(фирм, стран, домохозяйств) в один момент времени или в разные моменты в случае, когда время несущественно. Временные ряды – данные для одного объекта в различные моменты времени. Промежуточное положение занимают панельные данные, которые отражают наблюдения по большому числу объектов за небольшое число моментов времени, например,прибыли предприятий Казахстана за последние три года.
Случайной переменной называется переменная, которая с определенной вероятностью может принимать значения из каждого заданного множества.
Различают дискретные и непрерывные случайные величины. Если случайная величина может принимать конечное или счетное число значений, то это дискретная случайная величина. Пример – сумма выпавших очков при бросании двух игральных костей; число телевизоров, проданных в магазине за один день. Ее можно задать в виде таблицы
| x | 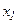
| 
| …. | 
|
| p | 
| 
| …. | 
|
где 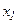 ,
,  , …
, …  - все значения, которые может принимать случайная величина х с вероятностями
- все значения, которые может принимать случайная величина х с вероятностями 
 …
…  соответственно.
соответственно.
При этом 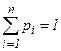 .
. 
Случайная величина, которая может принимать любые значения из некоторого интервала, является непрерывной случайной величиной. Пример –температура в комнате; максимальный биржевой курс доллара на торгах в течение дня. Она задается функцией плотности вероятности, принимающей неотрицательные значения.
Вероятность попадания случайной величины х в интервал [а,b] равна
 .
.
Эта площадь под кривой плотности вероятности  на отрезке a,b. Поскольку какое-либо значение х реализуется, то
на отрезке a,b. Поскольку какое-либо значение х реализуется, то  .
.
Особое значение имеет нормальное распределение вероятности.
Центральная предельная теорема утверждает, что если случайную величину можно представить как сумму большого числа не зависящих друг от друга слагаемых, каждое из которых вносит в сумму незначительный вклад, то эта сумма распределена приблизительно по нормальному закону.
Математическое ожидание случайной величины. Свойства математического ожидания. Математическое ожидание дискретной случайной величины – это взвешенное среднее всех ее возможных значений на вероятность соответствующего исхода. Математически если случайную величину обозначить как х, то ее математическое ожидание будет обозначаться как  .
.
Предположим, что х может принимать n конкретных значений ( ) и что вероятность получения
) и что вероятность получения  равна
равна 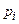 . Тогда математическое ожидание дискретной случайной величины равна
. Тогда математическое ожидание дискретной случайной величины равна
 (1)
(1)
и непрерывной случайной величины:  .
.
Например для распределения
| х | 1 | 3 | 5 |
| р | 0,3 | 0,5 | 0,2 |
Математическое ожидание Е(х)= 1*0,3+3*0,5*5*0,2=2,8.
Математическое ожидание случайной величины называют ее средним по генеральной совокупности. Совокупность всех возможных значений случайной переменной описывается генеральной совокупностью, из которой извлекаются эти значения. Для случайной величины х это значение часто обозначатся как  .
.
Свойства 1. Математическое ожидание суммы случайных величин равно сумме их математических ожиданий, т.е.
 (2)
(2)
Свойства 2. Если случайная переменная умножается на константу, то ее математическое ожидание умножается на ту же константу. Если х – случайная переменная и а – константа, то
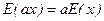 (3)
(3)
Свойства 3. Математическое ожидание константы есть сама эта величина, т.е. 
Теоретическая дисперсия Дисперсией (теоретической) случайной величины х называется математическое ожидание квадрата отклонения х от математического ожидания  , т.е.
, т.е.
 (4)
(4)
следовательно, для дискретной случайной величины
 ,
,
а для непрерывной случайной величины
 .
.
Пример расчета дисперсии для дискретной случайной величины  ,
,  .
.
 -теоретическое стандартное отклонение вычисляется путем простого извлечения из нее квадратного корня.
-теоретическое стандартное отклонение вычисляется путем простого извлечения из нее квадратного корня.
Положительное значение  свидетельствует о наличии прямой статистической связи между х,у, а отрицательное значение
свидетельствует о наличии прямой статистической связи между х,у, а отрицательное значение  - об обратной статистической связи между х,у.
- об обратной статистической связи между х,у.
Вероятность в непрерывном случае.
Дискретные случайные переменные по определению принимают значения из некоторого конечного набора. Каждое из этих значений связано с определенной вероятностью, характеризующей его «вес». Если эти «веса» известны, то не составит труда рассчитать теоретическое среднее(математическое ожидание) и дисперсию.
Вы можете представить указанные «веса» как определенные количества «пластичной массы», равные вероятностям соответствующих значений. Сумма вероятностей и, следовательно, суммарный «вес» этой массы равен «единице».
Более подробно рассмотрим анализ для непрерывных случайных величин, которые могут принимать бесконечное число значений.
Проиллюстрируем наши рассуждения на примере температуры в комнате. Для определенности предположим, что меняется в пределах от 55 до 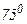 по Фаренгейту, и вначале допустим, что значения в этом диапазоне равновероятны.(рисунок 1).
по Фаренгейту, и вначале допустим, что значения в этом диапазоне равновероятны.(рисунок 1).
 |
|
В этом примере, мы будем предполагать, что «пластичная масса размазана» на единичной площади. Это связано с тем совокупная вероятность всегда равняется единице. В данном случае наша «масса» покрыла прямоугольник, и поскольку основание этого прямоугольника равно 20, его высота определяется из соотношения: 20 х Высота=1, так как произведение основания и высоты равно площади. Следовательно, высота равна 0,05.
 Найдя высоту прямоугольника, мы можем ответить на вопросы типа: с какой вероятностью температура будет находиться в диапазоне от 65 до
Найдя высоту прямоугольника, мы можем ответить на вопросы типа: с какой вероятностью температура будет находиться в диапазоне от 65 до  F? Ответ определяется величиной «замазанной» площади, лежащей в диапазоне от 65 до
F? Ответ определяется величиной «замазанной» площади, лежащей в диапазоне от 65 до  F, представленной заштрихованной фигурой на рисунке 2. Основание прямоугольника равно 5, его высота равна 0,05 и, соответственно, площадь –0,25. Искомая вероятность равна
F, представленной заштрихованной фигурой на рисунке 2. Основание прямоугольника равно 5, его высота равна 0,05 и, соответственно, площадь –0,25. Искомая вероятность равна  , что в любом случае очевидно, поскольку промежуток от 65 до
, что в любом случае очевидно, поскольку промежуток от 65 до  F составляет
F составляет  всего диапазона.
всего диапазона.
|
Высота заштрихованной площади представляет то, что формально называется плотностью вероятности в той точке, и если эта высота может быть записана как функция значений случайной переменной, то эта функция называется функцией плотности вероятности. В нашем примере она записывается как  , где х -температура, и
, где х -температура, и  .
.
В качестве первого приближения функция плотности вероятности показывает вероятность нахождения случайной переменной внутри единичного интервала вокруг данной точки. В нашем примере эта функция всюду равна 0,05, откуда вытекает, что температура находится, например, между 60 и  F с вероятностью 0,05.
F с вероятностью 0,05.
В нашем случае график функции плотности вероятности горизонтален, и ее указанная интерпретация точна, однако в общем случае эта функция непрерывно меняется, и ее интерпретация дает лишь приближение. Далее мы рассмотрим пример, когда эта функция непостоянна, поскольку не все температуры равновероятны. Предположим, что центральное отопление работает таким образом, что температура никогда не падает ниже  F, а в жаркие дни температура превосходит этот уровень, не превышая, как и ранее,
F, а в жаркие дни температура превосходит этот уровень, не превышая, как и ранее,  F. Мы будем считать, что плотность вероятности максимальна при температуре
F. Мы будем считать, что плотность вероятности максимальна при температуре  F и далее она равномерно убывает до нуля при
F и далее она равномерно убывает до нуля при  F.
F.
Общая «замазанная» площадь равен единице, поскольку совокупная вероятность равна единице. Площадь треугольника равна половине произведения основания на высоту, получаем: 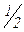 х 10 х Высота =1 и высота при
х 10 х Высота =1 и высота при  F равна 0,20.
F равна 0,20.
Предположим вновь, что мы хотим знать вероятность нахождения температуры в промежутке между 65 и  . Она представлена заштрихованной площадью на рисунке 3, и равна 0,75. Если вы предпочитаете процентное измерение, то это означает, что с вероятностью 75% температура попадает в диапазон 65 -
. Она представлена заштрихованной площадью на рисунке 3, и равна 0,75. Если вы предпочитаете процентное измерение, то это означает, что с вероятностью 75% температура попадает в диапазон 65 -  и только с вероятностью 25%- в диапазон 70-
и только с вероятностью 25%- в диапазон 70-  .
.
 В данном случае функция плотности вероятности равна
В данном случае функция плотности вероятности равна 
 .
.




 |
Основная литература: 1[3-8]
Дополнительная литература: 1[5-6]
Контрольные вопросы:
1.Дайте определение эконометрики.
2.Приведите основные типы статистических данных.
3.Дайте определение случайной величины.
4. Какой типичный вид графика функции плотности вероятности непрерывной случайной величины.
5.Дайте определение математическому ожиданию.
6.Дайте определение функции плотности вероятности.
Тема лекции 2.Постоянная и случайная составляющие случайной переменной. Несмещенность. Эффективность. Состоятельность. Выборочная ковариация. Дисперсия. Коэффициент корреляция
Конспект лекции: Часто вместо рассмотрения случайной величины как единого целого можно и удобно разбить ее на постоянную и чисто случайно составляющие, где постоянная составляющая всегда есть ее математическое ожидание. Если х – случайная переменная и m - ее математическое ожидание, то декомпозиция случайной величины записывается следующим образом:  , где u – чисто случайная составляющая.
, где u – чисто случайная составляющая.
Случайная составляющая u определяется как разность между х и m:  . Из определения следует, что математическое ожидание величины u равно нулю, а теоретическая дисперсия х равна теоретической дисперсии u.
. Из определения следует, что математическое ожидание величины u равно нулю, а теоретическая дисперсия х равна теоретической дисперсии u.
Способы оценивания и оценки. До сих пор мы предполагали, что имеется точная информация о рассматриваемой случайной переменной, в частности – об ее распределении вероятностей или функции плотности распределения. С помощью этой информации можно рассчитать теоретическое математическое ожидание, дисперсию и любые другие характеристики.
Однако на практике, за исключением искусственно простых случайных величин мы не знаем точного вероятностного распределения или плотности распределения вероятностей. Это означает, что неизвестны также и теоретическое математическое ожидание, и дисперсия. Мы, тем не менее, можем нуждаться в оценках этих или других теоретических характеристик генеральной совокупности.
Процедура оценивания всегда одинакова. Берется выборка из n наблюдений, и с помощью подходящей формулы рассчитывается оценка нужной характеристики.Способ оценивания – это общее правило, или формула, в то время как значение оценки – это конкретное число, которое меняется от выборки к выборке.
Приведем формулы оценивания для двух важнейших характеристик генеральной совокупности:
выборочное среднее -  ;
;
выборочное дисперсия случайной величины -  .
.
Оценки как случайные величины. Несмещенность. Эффективность. Состоятельность
Получаемая оценка представляет частный случай случайной переменной. Причина здесь в том, что сочетание значений х в выборке случайно, поскольку х- случайная переменная и, следовательно, случайной величиной является и функции набора ее значений. Возьмем, например  - оценку математического ожидания:
- оценку математического ожидания:
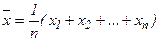 (5)
(5)
Мы только, что показали, что величина х а i-м наблюдении может быть разложен на две составляющие: постоянную часть m и чисто случайную составляющую ui:
 (6)
(6)
Следовательно,  (7)
(7)
где  -выборочное среднее величин ui.
-выборочное среднее величин ui.
Отсюда можно видеть, что  , подобно х, имеет фиксированную, та и чисто случайную составляющие. Ее фиксированная составляющая -m, то есть математическое ожидание х, а ее случайная составляющая -
, подобно х, имеет фиксированную, та и чисто случайную составляющие. Ее фиксированная составляющая -m, то есть математическое ожидание х, а ее случайная составляющая - 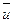 , то есть среднее значение чисто случайной составляющей в выборке.
, то есть среднее значение чисто случайной составляющей в выборке.
Величина  - оценка теоретической дисперсии х – также является случайной переменной. Вычитая (7) из (6), имеем:
- оценка теоретической дисперсии х – также является случайной переменной. Вычитая (7) из (6), имеем:
 (8)
(8)
следовательно,  .
.
Таким образом, s2 зависит от чисто случайной составляющей наблюдений х в выборке.
Полученная тем или иным способом оценка характеристики случайной величины сама является случайной величиной, так как она основывается на случайных реализациях переменной.
Оценка характеристики случайной величины называется несмещенной, если ее математическое ожидание совпадает с теоретическим значением этой характеристики.
Например, оценкой для математического ожидания может  может служить среднее выборочное
может служить среднее выборочное  . Имеем
. Имеем  .
.
Значит,  - несмещенная оценка для математического ожидания m случайной величины х.
- несмещенная оценка для математического ожидания m случайной величины х.
Эффективная оценка – это та, у которой дисперсия минимальна. Сейчас мы рассмотрим дисперсию обобщенной оценки теоретического среднего и покажем, что она минимальна в том случае, когда оба наблюдения имеют равные веса.
Если наблюдения  и
и  независимы, теоретическая дисперсия обобщенной оценки равна:
независимы, теоретическая дисперсия обобщенной оценки равна:
 (9)
(9)
Мы уже выяснили, что для несмещенности оценки необходимо равенство единице суммы  и
и  . Следовательно, для несмещенных оценок
. Следовательно, для несмещенных оценок  и
и

Поскольку мы хотим выбрать  так, чтобы минимизировать дисперсию, нам нужно минимизировать при этом (
так, чтобы минимизировать дисперсию, нам нужно минимизировать при этом ( ). Минимум достигается при
). Минимум достигается при 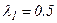 . Следовательно,
. Следовательно,  =0.5.
=0.5.
Итак, мы показали, выборочное среднее имеет наименьшую дисперсию среди оценок рассматриваемого типа. Это означает, что оно имеет наиболее «сжатое» вероятностное распределение вокруг истинного среднего и, следовательно наиболее точно. Строго говоря, выборочное среднее – это наиболее эффективная оценка среди всех несмещенных оценок.
Если предел оценки по вероятности равен истинному значению характеристики генеральной совокупности, то эта оценка называется состоятельной.
Тот факт, что при увеличении размера выборки распределение становится симметричным вокруг истинного значения, указывает на асимптотическую несмещенность. То, что в конечном счете оно превращается в единственную точку истинного значения, говорит о состоятельности оценки.
Выборочная ковариация. Дисперсия. Коэффициент корреляция
Выборочная ковариация является мерой взаимосвязи между двумя переменными.
При наличии n наблюдений двух переменных (х и у) выборочная ковариация между х и у задается формулой:
 . (10)
. (10)
Правила расчета ковариации.
1. Если  , то
, то 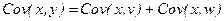 .
.
2. Если  , где а – константа, то
, где а – константа, то  .
.
3. Если 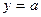 , где а – константа, то
, где а – константа, то  .
.
Пример. В период между 1963 и 1972 потребительский спрос на бензин устойчиво повышался. Эта тенденция прекратилась в 1973г., а затем последовали нерегулярные колебания спроса с незначительным его падением в целом. В табл. Приведены данные о потребительском спросе и реальных ценах после нефтяного кризиса. На рисунке 4 эти данные показаны в виде диаграммы рассеяния. Можно видеть некоторую отрицательную связь между потребительским спросом на бензин и его реальной ценой.
| год | расходы | Индеск реальных цен |
| 1973 | 26,2 | 103,5 |
| 1974 | 24,8 | 127,0 |
| 1975 | 25,6 | 126,0 |
| 1976 | 26,8 | 124,8 |
| 1977 | 27,7 | 124,7 |
| 1978 | 28,3 | 121,6 |
| 1979 | 27,4 | 149,7 |
| 1980 | 25,1 | 188,8 |
| 1981 | 25,2 | 193,6 |
| 1982 | 25,6 | 173,9 |
Показатель выборочной ковариации позволяет выразить данную связь единичным числом. Для его вычисления мы сначала находим средние значения цены и спроса на бензин. Обозначив через р и спрос – через у, определяем  и
и  , которые для выборки оказываются равными соответственно 143,36 и 26,27. Затем для каждого года вычисляем отклонение величин р и у от средних и перемножаем их. Для первого года (р-
, которые для выборки оказываются равными соответственно 143,36 и 26,27. Затем для каждого года вычисляем отклонение величин р и у от средних и перемножаем их. Для первого года (р-  ) равно (103,5-143,36) или –39,86 и (у-
) равно (103,5-143,36) или –39,86 и (у-  ) составит 2.79. Проделаем это для всех годов выборки и возьмем среднюю величину, она и будет выборочной ковариацией.
) составит 2.79. Проделаем это для всех годов выборки и возьмем среднюю величину, она и будет выборочной ковариацией.
Средняя величина (-16,24) она является значением выборочной ковариации. В данном случае она отрицательна. Так это и должно быть. Отрицательная связь, как это имеет место в данном примере выражается отрицательной ковариацией, а положительная связь – положительной ковариацией.
Диаграмму рассеяния (рис)наблюдений делится на четыре части вертикальной и горизонтальной линиями, проведенными через  и
и  соответственно. Пересечение этих линий образует точку (
соответственно. Пересечение этих линий образует точку ( ,
,  ), которая показывает среднюю цену и средний спрос за период времени, соответствующий нашей выборке.
), которая показывает среднюю цену и средний спрос за период времени, соответствующий нашей выборке.
Для любого наблюдения, лежащего в квадранте А, значения реальной цены и спроса выше соответствующих средних значений. Для данных наблюдений как (р-  ), так и (у-
), так и (у-  ) являются положительными, а поэтому должно быть положительным и (р-
) являются положительными, а поэтому должно быть положительным и (р-  )(у-
)(у-  ),.
),.
| наблюдение | у | р | (р-  ) )
| (у-  ) )
| (р-  ) (у- ) (у-  ) )
|
| 1973 | 26,2 | 103,5 | -39,86 | -0,07 | 2,79 |
| 1974 | 24,8 | 127,0 | -16,36 | -1,47 | 24,05 |
| 1975 | 25,6 | 126,0 | -17,36 | -0,67 | 11,63 |
| 1976 | 26,8 | 124,8 | -18,56 | 0,53 | -9,84 |
| 1977 | 27,7 | 124,7 | -18,66 | 1,43 | -26,68 |
| 1978 | 28,3 | 121,6 | -21,76 | 2,03 | -44,17 |
| 1979 | 27,4 | 149,7 | 6,34 | 1,13 | 7,16 |
| 1980 | 25,1 | 188,8 | 45,44 | -1,17 | -53,16 |
| 1981 | 25,2 | 193,6 | 50,24 | -1,07 | -53,76 |
| 1982 | 25,6 | 173,9 | 30,54 | -0,67 | -20,46 |
| Сумма Среднее | 262,7 26,27 | 1433,6 143,36 | -162,44 -16,24 |
 | |||
 | |||
|
|


Рисунок 4. Спрос на бензин
Наблюдение таким образом, дает положительный вклад в ковариацию. Так, например, наблюдение за 1979 лежит в этом квадранте и (р-  )=6.34, (у-
)=6.34, (у-  )=1.13, а их произведение равно 7.16.
)=1.13, а их произведение равно 7.16.
Далее рассмотрим квадрант В. Здесь наблюдения имеют реальную цену ниже средней и спрос выше среднего. Поэтому (р-  ) отрицательно (у-
) отрицательно (у-  ) положительно, произведение (р-
) положительно, произведение (р-  )(у-
)(у-  ) отрицательно, и наблюдение вносит отрицательный вклад в ковариацию. Например, наблюдение за 1978 имеет (р-
) отрицательно, и наблюдение вносит отрицательный вклад в ковариацию. Например, наблюдение за 1978 имеет (р-  )=-21,76, (у-
)=-21,76, (у-  )=2.03 и (р-
)=2.03 и (р-  )(у-
)(у-  )=-44,17.
)=-44,17.
В квадранте С как реальная цена, так и спрос ниже своих средних значений. Таким образом, (р-  ) и (у-
) и (у-  ) оба являются отрицательными, (р-
) оба являются отрицательными, (р-  )(у-
)(у-  ) положительно.
) положительно.
Наконец, в квадранте D реальная цена выше средней, а спрос ниже среднего. Таким образом, (р-  ) положительно (у-
) положительно (у-  ) отрицательно, поэтому (р-
) отрицательно, поэтому (р-  )(у-
)(у-  ) отрицательно, и в ковариацию, соответственно, вносится отрицательный вклад.
) отрицательно, и в ковариацию, соответственно, вносится отрицательный вклад.
Поскольку выборочная ковариация является средней величиной произведения
(р-  )(у-
)(у-  ) для 20 наблюдений, она будет положительной, если положительные вклады будут доминировать на отрицательными, и отрицательной, если будут отрицательные вклады. Положительные вклады исходят из квадрантов А и С, и ковариация будет, скорее всего, положительной, если основной разброс пойдет по наклонной вверх. Точно так же отрицательные вклады исходят из квадрантов В и D. Поэтому если основное рассеяние идет по наклонной вниз, как в данном примере, то ковариация будет, скорее всего отрицательной.
) для 20 наблюдений, она будет положительной, если положительные вклады будут доминировать на отрицательными, и отрицательной, если будут отрицательные вклады. Положительные вклады исходят из квадрантов А и С, и ковариация будет, скорее всего, положительной, если основной разброс пойдет по наклонной вверх. Точно так же отрицательные вклады исходят из квадрантов В и D. Поэтому если основное рассеяние идет по наклонной вниз, как в данном примере, то ковариация будет, скорее всего отрицательной.
Если х и у – случайные величины, то теоретическая ковариация  определяется как математическое ожидание произведения отклонений этих величин от их средних значений:
определяется как математическое ожидание произведения отклонений этих величин от их средних значений:

где  и
и  - теоретические средние значения х и у соответственно.
- теоретические средние значения х и у соответственно.
Для выборки из n наблюдений 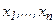 выборочная дисперсия определяется как среднеквадратичное отклонение в выборке:
выборочная дисперсия определяется как среднеквадратичное отклонение в выборке:  .
.
Правила расчета дисперсии
1.Если  , то
, то  .
.
2. Если  , где а является постоянной, то
, где а является постоянной, то 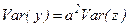 .
.
3. Если 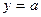 , где а является постоянной, то
, где а является постоянной, то 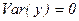 .
.
4. Если  , где а является постоянной, то
, где а является постоянной, то  .
.
Более точной мерой зависимости является коэффициент корреляции. Коэффициент корреляции имеет две формы – теоретическую и выборочную. Теоретический коэффициент корреляции r определяется следующим образом: 
Выборочный коэффициент корреляции r определяется путем замены теоретических дисперсий и ковариации на их несмещенные оценки.
 .
.
Выборочный коэффициент корреляции имеет максимальное значение, равное единице, которое получается при строгой линейной положительной зависимости между выборочными значениями х и у. Аналогичным образом r принимает минимальное значение –1, когда существует линейная отрицательная зависимость. Величина r =0 показывает. Что зависимость между наблюдениями х и у в выборке отсутствует.
Основная литература: 1[34-48]
Дополнительная литература:6[55-57]
Контрольные вопросы:
1. Что такое чисто случайная составляющая u?
2. Что такое оценка?
3. Для чего нужен способ оценивания?
4. Какая оценка называется эффективной?
5. Какая оценка называется несмещенной?
6. Какая оценка называется состоятельная?
7. Что такое выборочное среднее.
8. Что такое выборочная, теоретическая ковариация?
9. Что такое выборочная дисперсия?
10. Какие две формы имеет коэффициент корреляции?
11. Правила расчета ковариации, дисперсии.
12. Что означает r =0.
Тема лекции 3. Модель парной линейной регрессии. Регрессия по методу наименьших квадратов. Коэффициент детерминации  .
.
Конспект лекции: Слово «парная» означает, что рассматривается зависимость между двумя переменными. Если отклонения точек наблюдения от некоторой прямой линии случайные и небольшие, как на рисунке 5, то скорее всего мы имеем дело с линейной регрессией.
Для двух переменных х,у модель парной линейной регрессии имеет вид  ,
,
 |
· ·
· · · ·
· ·
Рисунок 5
где a, b - коэффициенты, параметры модели, e - случайный член. При этом х – объясняющая переменная, а у – зависимая переменная.
Включение в модель случайного члена, связано с возмущениями, которые не учтены в данной модели, например: нелинейность зависимости, наличие других переменных, не учтенных в модели, неправильный выбор объясняющей переменной, ошибки измерений, агрегирование переменных.
Коэффициенты a, b уравнения регрессии не известны. В качестве грубой аппроксимации мы можем сделать это, отложив четыре точки Р и построив прямую, в наибольшей степени соответствующую этим точкам. Как показано на рисунке 6. Отрезок, отсекаемый прямой на оси у, представляет собой оценку a и обозначен а, а угловой коэффициент прямой представляет собой оценку b и обозначен b.

Рисунок 6 –Прямая, построенная по точкам
С самого начала необходимо признать, что вы никогда не сможете рассчитать истинные значения a и b при попытке построить прямую и определить положение линии регрессии. Вы можете получить только оценки, и они могут быть хорошими или плохими.
Первым шагом является определение остатка для каждого наблюдения. За исключением случаев чистого совпадения, построенная вами линия регрессии не пройдет точно ни через одну точку наблюдения. Например, на рисунке 7 при х=х1 соответствующей ему точкой на линии регрессии будет R1со значением у, которое мы обозначим  вместо
вместо

Рисунок 7
фактически наблюдаемого значения у1 . Величина  описывается как расчетное значение у, соответствующее х1. Разность между фактическим и расчетным значениями (у1 -
описывается как расчетное значение у, соответствующее х1. Разность между фактическим и расчетным значениями (у1 -  ), определяемая отрезком Р1R1, описывается как остаток в первом наблюдении. Обозначим его е1. Соответственно, для других наблюдений остатки будут обозначены как е2, е3 и е4.
), определяемая отрезком Р1R1, описывается как остаток в первом наблюдении. Обозначим его е1. Соответственно, для других наблюдений остатки будут обозначены как е2, е3 и е4.
Очевидно, что мы хотим построить линию регрессии таким образом, чтобы эти остатки были минимальными. Очевидно также, что линия, строго соответствующая одним наблюдениям, не будет соответствовать другим, и наоборот. Необходимо выбрать какой-то критерий подбора, который будет одновременно учитывать величину всех остатков.
Существует целый ряд возможных критериев, одни из которых «работают» лучше других. Например, бесполезно минимизировать сумму остатков. Сумма будет автоматически равна нулю, если вы сделаете a равным  , а b равным нулю, получив горизонтальную линию у=
, а b равным нулю, получив горизонтальную линию у=  . В этом случае положительные остатки точно уравновесят отрицательные, но строгой зависимости при этом не будет.
. В этом случае положительные остатки точно уравновесят отрицательные, но строгой зависимости при этом не будет.
Одним из способов решения поставленной проблемы состоит в минимизации суммы квадратов остатков S:
 .
.
Величина S будет зависеть от выбора а и b, так как они определяют положение линии регрессии. В соответствии с этим критерием, чем меньше S, тем строже соответствие. Если S=0, то получено абсолютно точное соответствие, так как это означает, что все остатки равны нулю. В этом случае линия регрессии будет проходить через все точки, однако, вообще говоря, это невозможно из-за наличия случайного члена.
Существуют и другие достаточно разумные решения, однако при выполнении определенных условий метод наименьших квадратов дает несмещенные и эффективные оценки a и b. По этой причине метод наименьших квадратов является наиболее популярным в водном курсе регрессионного анализа.
Пример. Дано наблюдаемое значение у=3, когда х=1, и у=5 при х=2. Оценим коэффициенты а и b уравнения 
| х | у | 
| е |
| 1 | 3 | a+b | 3-a-b |
| 2 | 5 | a+2b | 5-a-2b |

теперь мы хотим выбрать такие значения а и b, чтобы значение S было минимальным. Для этого используется дифференциальное исчисление и находим значения a и b, удовлетворяющие следующим соотношениям:
 ;
;  ;
;  ;
; 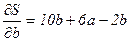 .
.
Таким образом, мы имеем: 2a+3b-8=0; 3a+5b-13=0.
Решив эти уравнения, получим a=1 и b=2. Следовательно, уравнение регрессии будет иметь следующий вид:  . Для того чтобы проверить, что мы пришли к правильному выводу, вычислим остатки: е1=3-a-b=3-1-2=0; e2=5-a-2b=5-1-4=0.
. Для того чтобы проверить, что мы пришли к правильному выводу, вычислим остатки: е1=3-a-b=3-1-2=0; e2=5-a-2b=5-1-4=0.
Таким образом, оба остатка равны нулю, что означает, что линия регрессии проходит точно через обе точки.
Коэффициент детерминации 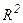 .
.
Регрессия по методу наименьших квадратов с одной независимой переменной.
Рассмотрим случай, когда имеется n наблюдений двух переменных х и у Предположив, что у зависит от х, мы хотим подобрать уравнение  .Мы хотим выбрать а и b, чтобы минимизировать величину S:
.Мы хотим выбрать а и b, чтобы минимизировать величину S: 
Необходимые условия минимума S заключается в равенстве нулю частных производственных по а и b:
 ,
,

Решение этой системы двух уравнений с двумя неизвестными дают формулы:
 ,
,  .
.
В парном регрессионном анализе поведение зависимой переменной объясняется поведением независимой переменной. Согласно определению остатков можно записать 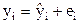 ,
,  .
.
Оказывается справедливо следующее равенство 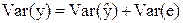 .
.
Это означает, что мы можем разложить Var(y) на две части:  - часть, которая «объясняется» уравнением регрессии и Var(e) – «необъясненную» часть.
- часть, которая «объясняется» уравнением регрессии и Var(e) – «необъясненную» часть.
Отношение  - это часть дисперсии у, объясненная уравнением регрессии. Это отношение известно как коэффициент детерминации, и его обычно обозначают
- это часть дисперсии у, объясненная уравнением регрессии. Это отношение известно как коэффициент детерминации, и его обычно обозначают 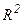 :
:
 , что равносильно
, что равносильно  .
.
Максимальное значение коэффициента 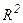 равно единице. Это происходит в том случае, когда линия регрессия точно соответствует всем наблюдениям, так что
равно единице. Это происходит в том случае, когда линия регрессия точно соответствует всем наблюдениям, так что  для всех I и все остатки равны нулю. Тогда
для всех I и все остатки равны нулю. Тогда  ,
,  и
и 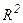 = 1.
= 1.
Если в выборке отсутствует видимая связь между у и х, то коэффициент 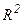 будет близок к нулю.
будет близок к нулю.
Свойства оценок по МНК. 4 –е условия Гаусса-Маркова
Свойства коэффициентов регрессии существенным образом зависят от свойств случайной составляющей. Для того, чтобы регрессионный анализ, основанный на методе наименьших квадратов, давал наилучшие из всех возможных результатов, случайный член должен удовлетворять четырем условиям, известным как условия Гаусса-Маркова
1-е условие. Математическое ожидание случайного члена равно нулю,  .
.
Случайный член u не должен иметь систематического отклонения ни в одном, ни в другом направлении.
2-е условие. Дисперсия случайного члена u постоянна для всех наблюдений, т.е.  .Сама величина
.Сама величина 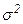 заранее неизвестна. Если дисперсия
заранее неизвестна. Если дисперсия  может меняться от наблюдения к наблюдению, то это условие Гаусса-Маркова нарушается.
может меняться от наблюдения к наблюдению, то это условие Гаусса-Маркова нарушается.
3-е условие. Случайные члены во всех наблюдениях должны быть независимы друг от друга.
В силу того, что  или
или  . (
. ( ).
).
Если это условие не будет выполнено, то регрессия, оцененная по методу наименьших квадратов, вновь не даст неэффективные результаты.
4-е условие. Случайный член должен быть распределен независимо от объясняющих переменных. Если х, как предполагалось неслучайная величина, должно быть  ,
,  .
.
В дополнение к этим четырем условиям делается предположение о нормальности распределения вероятности для случайного члена:  ,
,  .
.
Опираясь на условия Гаусса-Маркова, можно доказать следующие свойства коэффициентов a,b:
1.Величины а,b являются несмещенными оценками коэффициентов a, b соответственно уравнения парной линейной регрессии, т.е. 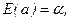
 .
.
2.Величины а, b являются эффективными оценками коэффициентов a, b соответственно, т.е. соблюдает наименьшей вариацией среди всех линейных несмещенных оценок этих коэффициентов.
Несмещенность коэффициентов регрессии.
На основании уравнения  можно показать, что b будет несмещенной оценкой β, если выполняется 4-е условие Гаусса - Маркова:
можно показать, что b будет несмещенной оценкой β, если выполняется 4-е условие Гаусса - Маркова:
 (11)
(11)
так как β - константа. Если мы примем сильную форму 4-го условия Гаусса-Маркова и предположим, что x - неслучайная величина, мы можем также считать Vаr(x) известной константой и, таким образом,
 (12)
(12)
Далее, если x - неслучайная величина, то Е{Cov(x,u)}=0 и, следовательно,
Е{b} = β. (13)
Таким образом, b - несмещенная оценка β.
За исключением того случая, когда случайные факторы в n наблюдениях в точности «гасят» друг друга, что может произойти лишь при случайном совпадении, b будет отличаться от β в каждом конкретном эксперименте. Однако с учетом соотношения (13) не будет систематической ошибки, завышающей или занижающей оценку. То же самое справедливо и для коэффициента a.
Точность коэффициентов регрессии.
Рассмотрим теперь теоретические дисперсии оценок a и b. Они задаются следующими выражениями:
 и
и  (14)
(14)
Из уравнения (14) можно сделать три очевидных заключения. Во-первых, дисперсии a и b прямо пропорциональны дисперсии остаточного члена  . Чем больше фактор случайности, тем хуже будут оценки при прочих равных условиях. Чем большей информацией вы располагаете, тем более точными, вероятно, будут ваши оценки. В-третьих, чем больше дисперсия x, тем меньше будет дисперсия коэффициентов регрессии. В чем причина этого? Чем меньше дисперсия x, тем больше, вероятно, будет относительное влияние фактора случайности при определении отклонений y и тем более вероятно, что регресcионный анализ может оказаться неверным. В действительности, как видно из уравнения (14), важное значение имеет не абсолютная, а относительная величина
. Чем больше фактор случайности, тем хуже будут оценки при прочих равных условиях. Чем большей информацией вы располагаете, тем более точными, вероятно, будут ваши оценки. В-третьих, чем больше дисперсия x, тем меньше будет дисперсия коэффициентов регрессии. В чем причина этого? Чем меньше дисперсия x, тем больше, вероятно, будет относительное влияние фактора случайности при определении отклонений y и тем более вероятно, что регресcионный анализ может оказаться неверным. В действительности, как видно из уравнения (14), важное значение имеет не абсолютная, а относительная величина  и Var(x).
и Var(x).
На практике мы не можем вычислить теоретические дисперсии a или b, так как 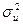 неизвестно, однако мы можем получить оценку
неизвестно, однако мы можем получить оценку  на основе остатков. Очевидно, что разброс относительно линии регрессии будет отражать неизвестный разброс u относительно линии y = α +β x, хотя в общем остаток и случайный член в любом данном наблюдении не равны друг другу. Следовательно, выборочная дисперсия остатков Var(e), которую мы можем измерить, сможет быть использована для оценки
на основе остатков. Очевидно, что разброс относительно линии регрессии будет отражать неизвестный разброс u относительно линии y = α +β x, хотя в общем остаток и случайный член в любом данном наблюдении не равны друг другу. Следовательно, выборочная дисперсия остатков Var(e), которую мы можем измерить, сможет быть использована для оценки 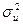 , которую мы получить не можем.
, которую мы получить не можем.
Прежде чем пойти дальше, задайте себе следующий вопрос: какая прямая будет ближе к точкам, представляющим собой выборку наблюдений по x и y: истинная прямая y = =α + β x или линия регрессии ŷ=a+bx? Ответ будет таков: линия регрессии, потому что по определению она строится таким образом, чтобы свести к минимуму сумму квадратов расстояний между ней и значениями наблюдений. Следовательно, разброс остатков у нее меньше, чем разброс значений u, и Var(e) имеет тенденцию занижать оценку  . Действительно, можно показать, что математическое ожидание Var(e), если имеется всего одна независимая переменная, равно [(n-2)/n]
. Действительно, можно показать, что математическое ожидание Var(e), если имеется всего одна независимая переменная, равно [(n-2)/n]  . Однако отсюда следует, что если определить
. Однако отсюда следует, что если определить  как
как
 =
= 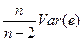 (15)
(15)
то  будет представлять собой несмещенную оценку
будет представлять собой несмещенную оценку  .
.
Используя уравнения (14) и (15), можно получить оценки теоретических дисперсий для a и b и после извлечения квадратного корня - оценки их стандартных отклонений. Вместо слишком громоздкого термина «оценка стандартного отклонения функции плотности вероятности» коэффициента регрессии будем использовать термин «стандартная ошибка» коэффициента регрессии, которую в дальнейшем мы будем обозначать в виде сокращения «с. о.» Таким образом, для парного регрессионного анализа мы имеем:
с.о.(a)=  и с.о.(b)=
и с.о.(b)=  (16)
(16)
Теорема Гаусса-Маркова. Предположим, что мы имеем зависимость, заданную уравнением y =α+β x + u и сосредоточим внимание на оценках для β. Человек, не знакомый с регрессионным анализом, увидев диаграмму разброса для выборки наблюдений, может попытаться получить оценку тангенса угла наклона путем простого объединения первого и последнего наблюдений и деления прироста высоты на горизонтальный отрезок между ними, Оценка b в этом случае будет определяться следующим образом:
 (17)
(17)
Каковы свойства этой оценки? Сначала исследуем, является ли она несмещенной. Используя уравнение y =α+β x + u применительно к первому и последнему наблюдениям, получим:
y1=α+βx1+u1 (18)
yn=α+βxn+un (19)
Следовательно,
 (20)
(20)
Таким образом, мы разложили «наивную» оценку на две составляющие: истинное значение и остаточный член. Предполагая Е(u) = 0, мы имеем, что математические ожидания, как u 1 так и un, равны нулю, но тогда математическое ожидание остаточного члена в уравнении (34) также равно нулю. Таким образом, несмотря на то, что эта оценка столь «наивна», она является несмещенной.
Это, разумеется, не единственная оценка, которая наряду с оценкой, полученной методом МНК, обладает свойством несмещенности. Вы можете получить еще одну оценку такого типа путем объединения двух произвольно выбранных наблюдений, а если вы хотите рассмотреть менее «наивные» процедуры, то здесь открываются поистине безграничные возможности.
Основная литература: 1[80-89]
Дополнительная литература: 6[71-78]
Контрольные вопросы:
1.Какой общий вид имеет модель парной линейной регрессии?
2.Перечислите основные причины существования случайного члена в модели парной линейной регрессии?
3.Какой метод используют для проведения регрессионного анализа?
4.В чем суть задачи регрессионного анализа?
5.Какое может принимать значение коэффициент детерминации и почему?
6.Для чего применяются четыре условия Гаусса-Маркова?
7.Перечислите все четыре условия Гаусса-Маркова и в чем их особенность?
8.Перечислите свойства коэффициентов а и b.
9. Что такое несмещенность?
10.Сформулируйте теорему Гаусса-Маркова.
Тема лекции 4. Проверка гипотез, относящихся к коэффициентам. Доверительные интервалы. Односторонние тесты.. F-тест на качество оценивания
Конспект лекции: В принципе, для любых результатов наблюдений  и
и  можно рассчитать коэффициенты линейной регрессии а, b (не все хi должны совпадать друг с другом).
можно рассчитать коэффициенты линейной регрессии а, b (не все хi должны совпадать друг с другом).
Небольшие изменения в точках наблюдений могут существенно изменить значения оцененных коэффициентов а, b и, следовательно, заметно повлиять на оцененную зависимость 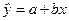 между двумя переменными.
между двумя переменными.
В какой мере можно доверять найденным значениям а,b? Для определенности будем вести речь и о коэффициенте b. Относительно коэффициента может быть в
|
|
 2020-01-15
2020-01-15 919
919








