Конспект лекции: Модель множественной линейной регрессии. Определение коэффициентов множественной линейной регрессии Теорема Гаусса-Маркова
Она задается уравнением вида
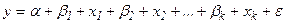 (23)
(23)
где у –зависимая переменная, x1, x2,…, xk – объясняющие переменные, e - случайный член,
a, b1, b2,…, bk – параметры, коэффициенты уравнения регрессии.
Требуется по данным наблюдений
| i | х1 | … | xk | y |
| 1 | х11 | … | xk1 | y1 |
| 2 | х12 | … | xk2 | y2 |
| .. | .. | .. | .. | .. |
| n | xkn | … | xkn | yn |
оценить параметры a,b1,…, bk. Число наблюдений n во всяком случае не должно быть меньше k+1.
Для данных значений х1i, х2i, хki объясняющих переменных значение уi зависимой переменной определяется реализацией eI случайного члена.
Предполагается выполненными условия Гаусса-Маркова и предположение о нормальности распределения вероятности для e.
Определение коэффициентов множественной линейной регрессии.
Пусть имеется выборка, состоящая из n наблюдении зависимой и объясняющих переменных уi, хi1, хi2, хin, i=1,2,…,n, для которых уравнение регрессии запишется в виде системы уравнений
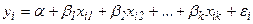 ,
, 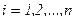 . (24)
. (24)
Определим векторы-столбцы и матрицу:
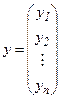 ,
, 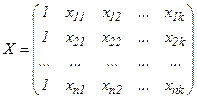 ,
, 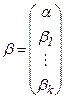 ,
, 
Столбец у и матрица х содержат данные выборки. В столбце b записаны неизвестные коэффициенты, которые следует оценить по имеющейся выборке, e- столбец случайных членов, которые не наблюдаемы.
Используя эти обозначения, систему уравнений (24) можно записать в компактной матричной форме: 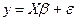 (25)
(25)
В модели множественной линейной регрессии метод наименьших квадратов представляет собой обобщение МНК для парной линейной регрессии. Оцененное уравнение множественной линейной регрессии
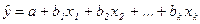 (26)
(26)
Запишем для всех наблюдений:  ,
, 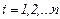 .
.
Их также можно записать в матричной форме:
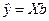 . (27)
. (27)
где столбцы 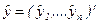 ,
,  .
.
Определим столбец отклонений фактических значений у зависимой переменной у от ее значений 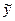 , вычисленных по оцененному уравнению регрессии (26):
, вычисленных по оцененному уравнению регрессии (26):
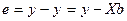 ,
, 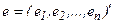 .
.
Метод наименьших квадратов заключается в определении коэффициентов оцененного уравнения (26) из условия минимума суммы квадратов отклонений: 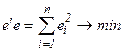 . На основе свойств операций над матрицами можем записать
. На основе свойств операций над матрицами можем записать
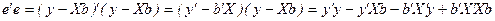 .
.
Это выражение зависит от вектора b и достигает минимума, если его производная по b равна нулевому вектору, т.е. 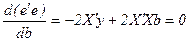 .
.
Если столбцы матрицы Х линейно независимы, то существует обратная матрица
(Х ’ Х)- 1 и можно найти оценку вектора b коэффициентов регрессии:  .
.
Он также обозначается через  . В случае k=1 отсюда можно получить оценки коэффициентов парной линейной регрессии.
. В случае k=1 отсюда можно получить оценки коэффициентов парной линейной регрессии.
Теорема Гаусса-Маркова
Если Х –детерминированная матрица n(k+1), имеющая полный ранг k+1, математическое ожидание Е(ε)=0, матрица ковариаций V(ε)=δ2In (In- обозначение единичной матрицы)- диагональная, то для модели линейной регрессии 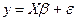 оценка метода наименьших квадратов
оценка метода наименьших квадратов 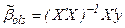 является эффективной среди всех несмещенных линейных оценок β.
является эффективной среди всех несмещенных линейных оценок β.
Это утверждение устанавливает обоснованность использования метода наименьших квадратов для оценки коэффициентов линейной регрессии.
При практическом построении модели линейной регрессии существенен вопрос о значимости ее коэффициентов, вычисленных по конкретной выборке. Сформулируем две гипотезы:
Нулевая Н0: 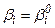 .
.
Альтернативная Н1:  .
.
Пусть 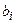 оценка коэффициента
оценка коэффициента 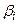 ,
, 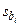 - стандартная ошибка оценки
- стандартная ошибка оценки  . Оказывается, величина
. Оказывается, величина 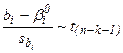 , т.е. имеет t-распределение Стьюдента с n-k-1 –степенями свободы, где n – число наблюдений, а k+1 – число оцениваемых коэффициентов уравнения (23), включая и свободный член.
, т.е. имеет t-распределение Стьюдента с n-k-1 –степенями свободы, где n – число наблюдений, а k+1 – число оцениваемых коэффициентов уравнения (23), включая и свободный член.
Для выбранного числа δ (уровня значимости) по таблице t распределения определяется критическое значение tc такое, что вероятность реализации 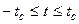 ,
, 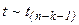 равна 1-δ. Затем проверяется условие
равна 1-δ. Затем проверяется условие 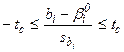 .Если оно не выполняется, то гипотеза Н0 отвергается, а при его выполнении Н0 не отвергается (принимается).Обычно коэффициент
.Если оно не выполняется, то гипотеза Н0 отвергается, а при его выполнении Н0 не отвергается (принимается).Обычно коэффициент 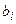 сравнивают с
сравнивают с 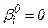 .
.
Свойства коэффициентов множественной регрессии
Как и в случае парного регрессионного анализа, коэффициенты регрессии должны рассматриваться как случайные переменные специального вида, случайные компоненты которых обусловлены наличием в модели случайного члена. Каждый коэффициент регрессии вычисляется как функция значений у и независимых переменных в выборке, а y в свою очередь определяется независимыми переменными и случайным членом. Отсюда следует, что коэффициенты регрессии действительно определяются значениями независимых переменных и случайным членом, а их свойства существенно зависят от свойств последнего.
Мы продолжаем считать, что выполняются условия Гаусса—Маркова, а именно:
1) математическое ожидание и в любом наблюдении равно нулю;
2) теоретическая дисперсия его распределения одинакова для всех наблюдений;
3) теоретическая ковариация его значений в любых двух наблюдениях равняется нулю;
4) распределение и независимо от распределения любой объясняющей переменной. Первые три условия идентичны условиям для парного регрессионного: анализа, а четвертое условие является обобщением своего аналога. На данный момент мы примем усиленный вариант четвертого условия, допустив, что независимые переменные являются нестохастическими.
Существуют еще два практических требования. Во-первых, нужно иметь достаточное количество данных для проведения линии регрессии, что означает наличие стольких (независимых) наблюдений, сколько параметров необходимо оценить. Во-вторых, как мы увидим далее в этом разделе, между независимыми переменными не должно существовать строгой линейной зависимости.
Несмещенность. Мы покажем, что b1является несмещенной оценкой B1 для случая с двумя объясняющими переменными. Доказательство можно легко обобщить, используя матричную алгебру для любого числа объясняющих переменных. Как видно уравнения, величина b1является функцией от х 1 х2 и у в свою очередь yопределяется по х1, х2 и и. Следовательно, величина b1фактически зависит от значений х 1, х2 и и в выборке (поняв суть преобразований, можно опуститьдетали математических выкладок):
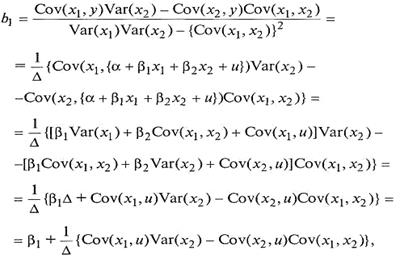
где Δ равно Var (x1)Var (x2) — {Cov (x1, x2)}2. Отсюда величина b1 имеет две составляющие: истинное значение β1 и составляющую ошибки. Перейдя к математическому ожиданию, получим:
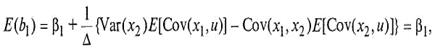
при допущении, что выполняется 4 условие Гаусса – Маркова.
Точность коэффициентов множественной регрессии
В теореме Гаусса—Маркова для множественного регрессионного анализа доказывается, что, как и для парной регрессии, обычный метод наименьших квадратов (МНК) дает наиболее эффективные линейные оценки в том смысле, что наоснове той же самой выборочной информации невозможно найти другие несмещенные оценки с меньшими дисперсиями при выполнении условий Гаусса—Маркова. Мы не будем доказывать эту теорему, но исследуем факторы, регулирующие возможную точность коэффициентов регрессии. В общем случае можно сказать, что коэффициенты регрессии, скорее всего, являются более точными:
1) чем больше число наблюдений в выборке;
2) чем больше дисперсия выборки объясняющих переменных;
3) чем меньше теоретическая дисперсия случайного члена;
4) чем меньше связаны между собой объясняющие переменные.
Первые три из желательных условий повторяют то, на чем мы уже останавливались в случае парного регрессионного анализа. Лишь четвертое условие является новым. Сначала мы рассмотрим случай с двумя независимыми переменными и затем перейдем к более общему случаю.
t-тесты для коэффициентов множественной регрессии выполняются так же, как это делается в парном регрессионном анализе. Отметим, что критический уровень t при любом уровне значимости зависит от числа степеней свободы, которое равно (n-k-1): число наблюдений минус число оцененных параметров. Доверительные интервалы определяются точно так же, как и в парном регрессионном анализе, в соответствии с указанием примечанием относительно числа степеней свободы.
Основная литература:1[134-148]
Дополнительная литература:3[60-65]
Контрольные вопросы:
1.Приведедите уравнение множественной линейной регрессии в матричной форме.
2.Сформулируйте теорему Гаусса- Маркова.
3.Каким образом проверяется значимость коэффициентов модели линейной регрессии.
4.Как определяется величина t –распределение Стьюдента.
5. Какие уровни значимости принимают.
6.Чем отличаются свойства множественной регрессии от парной.
7.Напишите формулу для несмещенной оценки b.
8. При каких условиях коэффициенты регрессии будут точными.
9. Что означает «чем меньше теоретическая дисперсия случайного члена».
10. Как определяется связь между объясняющими переменными
Тема лекции 6. Мультиколлинеарность. Качество оценивания: коэффициент R2.Гетероскедастичность и ее последствия. Автокорреляция и связанные с ней факторы.
Конспект лекции: Это явление означает коррелированность двух или нескольких объясняющих переменных в уравнении регрессии. Например, если в состав объясняющих переменных входят располагаемый доход и потребление, то обе эти переменные будут сильно коррелированными. Мультиколлинеарность может привести к незначимости коэффициентов регрессии.
Например, если в модели множественной линейной регрессии
 (27)
(27)
есть линейная связь между двумя переменными х1 и х2, пусть х2=gх1, то уравнение (27) может быть записан в виде
 (28)
(28)
где коэффициент  .
.
Можно ожидать получения значимых по t –статистике оценок для коэффициентов уравнения регрессии (28), т.е. для a, 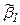 , b3 …bk . В частности, это может быть для коэффициента
, b3 …bk . В частности, это может быть для коэффициента 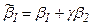 . Но для коэффициентов b1, b2 по отдельности получения значимых оценок невозможно. Это крайний случай строгой линейной зависимости между двумя объясняющими переменными.
. Но для коэффициентов b1, b2 по отдельности получения значимых оценок невозможно. Это крайний случай строгой линейной зависимости между двумя объясняющими переменными.
В случае, когда связь между переменными х1, х2 нестрогая, тем труднее разделить влияние объясняющих переменных, чем сильнее они коррелированны между собой.t-статистики коэффициентов при таких переменных будут получаться низкими.
Можно вывести корреляционную матрицу и определить пары переменных, сильно коррелированных между собой. Но возможно взаимовлияние объясняющих переменных модели между собой. Поэтому более правильно использовать матрицу частных коэффициентов корреляции.
Определить переменные, ответственные за мультиколлинеарность, можно также рассматривая каждую объясняющую переменную как зависимую от нескольких объясняющих переменных:
хi=d + q1 x1 +…+qj-1 xj-1 +qj+1xj-1 +…+qkxk +e. (29)
где d, q1,…,qj-1, qj+1, qk –коэффициенты этой вспомогательной регрессии, j=1,2,…k.
Чем ближе коэффициент детерминации  регрессии (44) к 1, тем в большей мере хj зависит от остальных факторов. Определив коэффициенты детерминации
регрессии (44) к 1, тем в большей мере хj зависит от остальных факторов. Определив коэффициенты детерминации 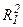 ,
, 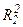 ,….,
,….,  можно, сравнивая их, указать на переменную, в наибольшей степени ответственную за возникновение мультиколлинеарности.
можно, сравнивая их, указать на переменную, в наибольшей степени ответственную за возникновение мультиколлинеарности.
Для устранения мультиколлинеарности можно исключить из уравнения одну или несколько объясняющих переменных, преобразовать переменные. Типичное преобразование – переход к первым разностям, особенно, для временных рядов, например, от х t к Dхt=xt- xt- 1, где t -момент времени.
Качество оценивания: коэффициент R2.
Как и в парном регрессионном анализе, коэффициент детерминации R2 определяет долю дисперсии у, объясненную регрессией, и эквивалентно определяется как величина
Var (у)/ Var (у), как {1 — Var (e)/ Var (у)} или как квадрат коэффициента корреляции между у и y. Этот коэффициент никогда не уменьшается (а обычно он увеличивается) при добавлении еще одной переменной в уравнение регрессии, если все ранее включенные объясняющие переменные сохраняются. Для иллюстрации этого предположим, что вы оцениваете регрессионную зависимость у от х1 и х2и получаете уравнение вида:
у = а + blxl + bx2 (30)
Далее, предположим, что вы оцениваете регрессионную зависимость у только от xl, в результате получив следующее:
y= a* + bl *xl (31)
Это уравнение можно переписать в виде:
y= a* + bl *xl +0 x2 (32)
Если сравнить уравнения (30) и (32), то коэффициенты в первом из них свободно определялись с помощью метода наименьших квадратов на основе данных для у, х1 и х2 при обеспечении наилучшего качества оценки. Однако в уравнении (32) коэффициент при х2 был произвольно установлен равным нулю, и оценивание не будет оптимальным, если только по случайному совпадению величина b2 не окажется равной нулю, когда оценки будут такими же. (В этом случае величина а* будет равна a, а величина b1* будет равна b1). Следовательно, обычно коэффициент R2 будет выше в уравнении (30), чем в уравнении (31), и он никогда не станет ниже. Конечно, если новая переменная на самом деле не относится к этому уравнению, то увеличение коэффициента R2 будет, вероятно, незначительным.
Вы можете решить, что поскольку коэффициент R2 измеряет долю дисперсии, совместно объясненной независимыми переменными, то можно определить отдельный вклад каждой независимой переменной и таким образом получить меру ее относительной важности. Было бы очень удобно, если бы это стало возможным. К сожалению, такое разложение невозможно, если независимые переменные коррелированы, поскольку их объясняющая способность будет перекрываться.
F-тесты. F-тест использовался для анализа дисперсии. Когда используем регрессионный анализ для деления дисперсии зависимой переменной на «объясненную» и «необъясненную» составляющие, можно построить F-статистику:
 ,
,
где ESS – объясненная сумма квадратов отклонений; RSS-остаточная (необъясненная) сумма квадратов; k-число степеней свободы, использованное на объяснение. С помощью этой статистики можно выполнить F-тест для определения того, действительно ли объясненная сумма квадратов больше той, которая может иметь место случайно. Для этого нужно найти критический уровень F в колонке, соответствующей k степеням свободы, и в ряду, соответствующем (n-k-1) степеням свободы.
Гетероскедастичность и ее последствия. Второе условие Гаусса-Маркова требует постоянства дисперсии случайного члена 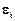 во всех наблюдениях:
во всех наблюдениях: 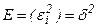 ,
, 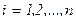 -гомоскедастичность
-гомоскедастичность
А если дисперсия случайного члена меняется от наблюдения к наблюдению, то мы имеем дело с гетероскедастичностью. 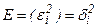 ,
, 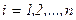
Во втором условии Гаусса – Маркова утверждается, что дисперсия случайного члена в каждом наблюдении должна быть постоянной. Такое утверждение может показаться странным, и здесь требуется пояснение. Случайный член в каждом наблюдении имеет только одно значение, и может возникнуть вопрос о том, что означает его “дисперсия”.
Имеется в виду его возможное поведение до того, как сделана выборка. Когда мы записываем модель
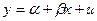 (33)
(33)
первые два условия Гаусса – Маркова указывают, что случайные члены 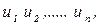 в n наблюдениях появляются на основе вероятных распределений, имеющих нулевое математическое ожидание и одну и ту же дисперсию. Их фактические значения в выборке иногда будут положительными, иногда – отрицательными, иногда – относительно далекими от нуля, иногда – относительно близкими к нулю, но у нас нет причин ожидать появления особенно больших отклонений в любом данном наблюдении. Другими словами, вероятность того, что величина u примет какое – то данное положительное (или отрицательное) значение, будет одинаковой для всех наблюдений. Это условие известно как гомоскедастичность, что означает “одинаковый разброс”.
в n наблюдениях появляются на основе вероятных распределений, имеющих нулевое математическое ожидание и одну и ту же дисперсию. Их фактические значения в выборке иногда будут положительными, иногда – отрицательными, иногда – относительно далекими от нуля, иногда – относительно близкими к нулю, но у нас нет причин ожидать появления особенно больших отклонений в любом данном наблюдении. Другими словами, вероятность того, что величина u примет какое – то данное положительное (или отрицательное) значение, будет одинаковой для всех наблюдений. Это условие известно как гомоскедастичность, что означает “одинаковый разброс”.
Вместе с тем для некоторых выборок, возможно, более целесообразно предположить, что теоретическое распределение случайного члена является разным для различных наблюдений в выборке. Дисперсия величины 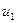 увеличивается по мере продолжения выборочных наблюдений. Это не означает, что случайный член обязательно будет иметь особенно большие (положительные или отрицательные) значения в конце выборке, но это значит, что априорная вероятность получения сильно отклоненных величин будет относительно высока. Это пример гетероскедастичности, что означает “неодинаковый разброс”. Математически гомоскедастичность и гетероскедастичность могут определяться следующим образом:
увеличивается по мере продолжения выборочных наблюдений. Это не означает, что случайный член обязательно будет иметь особенно большие (положительные или отрицательные) значения в конце выборке, но это значит, что априорная вероятность получения сильно отклоненных величин будет относительно высока. Это пример гетероскедастичности, что означает “неодинаковый разброс”. Математически гомоскедастичность и гетероскедастичность могут определяться следующим образом:
Гомоскедастичность: 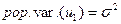 постоянна для всех наблюдений;
постоянна для всех наблюдений;
Гетероскедастичность: 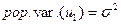 , она не обязательно одинакова для всех i.
, она не обязательно одинакова для всех i.
Возникает вопрос, почему гетероскедатичность имеет существенное значение. В самом деле, соответствующее условие Гаусса – Маркова пока не использовалось в проводимом анализе, и оно может показаться практически не нужным. В частности, при рассмотрении простой модели (33) и оцененного уравнения
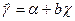 , (34)
, (34)
в доказательстве того, что b является несмещенной оценкой 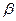 и
и 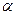 - несмещенной оценкой
- несмещенной оценкой 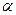 , это условие не использовалась.
, это условие не использовалась.
Это объясняется двумя причинами. Первая касается дисперсии оценок a и b. Желательно, чтобы она была как можно меньше, т.е. (в вероятностном смысле) обеспечивала максимальную точность. При отсутствие гетероскедатичности обычные коэффициенты регрессии имеют наиболее низкую дисперсию среди всех несмещенных оценок, являющихся линейными функциями от наблюдений у. Если имеет место гетероскедатичность, то оценки МНК, которые мы до сих пор использовали, неэффективны. Можно, по меньшей мере, в принципе, найти другие оценки, которые имеют меньшую дисперсию и, тем не менее, являются несмещенными.
Вторая, не менее важная причина заключается в том, что сделанные оценки стандартных ошибок коэффициентов регрессия будут неверны. Они вычисляются на основе предположения о том, что распределение случайного члена гомоскедатично: если это не так, то они неверны. Вполне вероятно, что стандартные ошибки будут занижены, а следовательно, 1 – статистика – завышена, и будет получено неправильное представление о точности оценки уравнения регрессии. Возможно, вы решите, что коэффициент значимо отличается от нуля при данном уровне значимости, тогда как в действительности это не так.
Свойство неэффективности можно легко объяснить интуитивно. Предложим, что имеется гетероскедастичность типа, наблюдение, для которого теоретическое распределение случайного члена имеет малое стандартное отклонение, будет обычно находится близко к линии регрессии 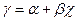 и, следовательно, может стать хорошим направляющим ориентиром, указывающим место этой линии. В противоположность этому наблюдению, где теоретическое распределение имеет большое стандартное отклонение, не сможет существенно помочь в определении местоположения линии регрессии. Обычный МНК не делает различия между качеством наблюдений, придавая одинаковые “веса” каждому из них независимо от того, является ли наблюдение хорошим или плохим для определения местоположения этой линии. Из этого следует, что, если мы сможем найти способ придания большего “веса” наблюдениям высокого качества и меньшего – наблюдениям низкого качества, мы, вероятно, получим более точные оценки. Другими словами, оценки для
и, следовательно, может стать хорошим направляющим ориентиром, указывающим место этой линии. В противоположность этому наблюдению, где теоретическое распределение имеет большое стандартное отклонение, не сможет существенно помочь в определении местоположения линии регрессии. Обычный МНК не делает различия между качеством наблюдений, придавая одинаковые “веса” каждому из них независимо от того, является ли наблюдение хорошим или плохим для определения местоположения этой линии. Из этого следует, что, если мы сможем найти способ придания большего “веса” наблюдениям высокого качества и меньшего – наблюдениям низкого качества, мы, вероятно, получим более точные оценки. Другими словами, оценки для 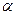 и
и 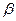 будут более эффективными.
будут более эффективными.
При гетероскедастичности коэффициенты регрессии будут несмещенными, но неэффективными. Вследствие этого окажутся завышенными t –статистики, и будут сделаны неверные выводы о значимости коэффициентов уравнения регрессии.
Существуют различные способы выявления герероскедатичности.
Тесты на гетероскедастичность. Существует несколько тестов на гетероскедастичность. Во всех этих тестах проверяется основная нулевая гипотеза о равенстве дисперсий 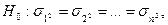 (наличие гомоскедастичности, отсутствие гетероскедастичности) против альтернативной гипотезы
(наличие гомоскедастичности, отсутствие гетероскедастичности) против альтернативной гипотезы  не
не 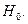
Тест ранговой корреляции Спирмена
При выполнении теста ранговой корреляции Спирмена предполагается, что дисперсия случайного члена будет либо увеличиваться, либо уменьшается по мере увеличения х, и поэтому в регрессии, оцениваемой с помощью МНК, абсолютные величины остатков и значения х будут коррелированы. Данные по х и остатки упорядочиваются, и коэффициент ранговой корреляции определяется как
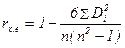 ,
,
где 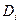 -разность между рангом х и рангом е.
-разность между рангом х и рангом е.
Рассмотрим один из самых распространенных тестов – тест Голдфелд-Квандта. При проведении проверки по этому критерию предполагается, что стандартное отклонение распределения вероятностей 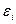 пропорционально значению х в этом наблюдении. Предполагается также, что случайный член распределен нормально и не подвержен автокорреляции.
пропорционально значению х в этом наблюдении. Предполагается также, что случайный член распределен нормально и не подвержен автокорреляции.
Все n наблюдений в выборке упорядочиваются по величине х, после чего оцениваются отдельные регрессии для первых 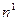 и для последних
и для последних 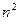 наблюдений: средние
наблюдений: средние 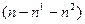 наблюдений отбрасываются. Если предположение относительно природы гетероскедастичности верно, то дисперсия
наблюдений отбрасываются. Если предположение относительно природы гетероскедастичности верно, то дисперсия 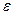 в последних
в последних 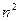 наблюдениях будет больше, чем в первых
наблюдениях будет больше, чем в первых 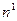 , и это будет отражено в сумме квадратов остатков в двух указанных «частных» регрессиях. Обозначая суммы квадратов остатков в регрессиях для первых
, и это будет отражено в сумме квадратов остатков в двух указанных «частных» регрессиях. Обозначая суммы квадратов остатков в регрессиях для первых 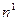 для последних
для последних 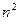 наблюдений соответственно через
наблюдений соответственно через 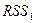 и
и  , рассчитаем отношение
, рассчитаем отношение 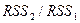 , которое имеет F-распределение с (n - m - 1) и
, которое имеет F-распределение с (n - m - 1) и 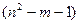 степенями свободы, где m – число объясняющих переменных в регрессионном уравнении. Мощность критерия зависит от выбора n по отношению к n. Основываясь на результатах некоторых проведенных ими экспериментов, С.Голфелд и Р.Квандт утверждают, что n должно составлять порядка 11, когда n=30, и порядка 22, когда n=60. Если в модели имеется более одной объясняющей переменной, то наблюдения должны упорядочиваться по той из них, которая, как предпологается, связана с
степенями свободы, где m – число объясняющих переменных в регрессионном уравнении. Мощность критерия зависит от выбора n по отношению к n. Основываясь на результатах некоторых проведенных ими экспериментов, С.Голфелд и Р.Квандт утверждают, что n должно составлять порядка 11, когда n=30, и порядка 22, когда n=60. Если в модели имеется более одной объясняющей переменной, то наблюдения должны упорядочиваться по той из них, которая, как предпологается, связана с 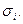
Тест Глейзера..Тест Глейзера позволяет несколько более тщательно рассмотреть характер гетероскедастичности. Мы снимаем предположение о том, что σ i пропорционально х i, и хотим проверить, может ли быть более подходящей какая-либо другая функциональная форма, например
σ i =α +βχ γi (35)
Чтобы использовать данный метод, следует оценить регрессионную зависимость у от х с помощью обычного МНК, а затем вычислить абсолютные величины остатков |е i | по функции (50) для данного значения у. Можно построить несколько таких функций, изменяя значение у. В каждом случае нулевая гипотеза об отсутствии гетероскедастичности будет отклонена, если оценка β значимо отличается от нуля. Если при оценивании более чем одной функции получается значимая оценка β, то ориентиром при определении характера гетероскедастичности может служить наилучшая из них.
Автокорреляция и связанные с ней факторы. Наряду с проверкой статистической значимости коэффициентов уравнения регрессии с помощью t-статистики и общего качества уравнения регрессии на основе коэффициентов детерминации 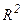 ,
,  и F –статистики Фишера необходима проверка выполнения условий Гаусса-Маркова. Их нарушение может привести к смещенности и неэффективности коэффициентов уравнения регрессии.
и F –статистики Фишера необходима проверка выполнения условий Гаусса-Маркова. Их нарушение может привести к смещенности и неэффективности коэффициентов уравнения регрессии.
Напомним, что третье условие Гаусса-Маркова при выполнении первого условия Е(ei ej)=0, i¹j, i, j=1,2,…n.
Оно отображает независимость случайных членов в разных наблюдениях.
При нарушении этого условия, т.е при наличии связи между случайными членами возникает явление автокорреляции.
В случае положительной автокорреляции реализации случайного члена для ряда последовательных наблюдений смещают значения зависимой переменной в одном направлении. Затем для нескольких последовательных наблюдений – в противоположенном направлении, потом снова в первоначальном направлении и т.д. В экономике положительная автокорреляция может связана с циклами деловой активности, с сезонными колебаниями, влияние которых и отражается в случайном члене уравнения регрессии.
При отрицательной автокорреляции каждая реализация случайного члена ei как правило, сменяется реализаций случайного члена ei+1 противоположного знака
Для экономики обычно характерно возникновение положительной автокорреляции, особенно, для временных рядов. Появление автокорреляции более вероятно для малых временных промежутков между наблюдениями.
В значительной части рядов динамики экономических процессов между уровнями, особенно близко расположенными, существует взаимосвязь. Ее удобно представить в виде корреляционной зависимости между рядами 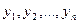 и этим же рядом, сдвинутым относительно первоначального положения на h моментов времени
и этим же рядом, сдвинутым относительно первоначального положения на h моментов времени  Смещение на время L называется сдвигом, а само явление взаимосвязи – автокорреляцией.
Смещение на время L называется сдвигом, а само явление взаимосвязи – автокорреляцией.
Автокорреляционная зависимость особенно существенна между последующими и предшествующими уровнями ряда динамики. Поскольку классические методы математической статистики применимы лишь в случае независимости отдельных членов ряда между собой, то при анализе нескольких взаимосвязанных рядов динамики важно установить наличие и степень их автокорреляции.
Различаются два вида автокорреляции:
1) автокорреляция в наблюдениях за одной или более переменными;
2) автокорреляция ошибок, или автокорреляция в отклонениях от регрессионной модели.
Наличие последней приводит к искажению величин средних квадратических ошибок коэффициентов регрессии, что затрудняет проверку их значимости.
Автокорреляция в наблюдениях за одной или более переменными. Автокорреляцию измеряют при помощи нециклического коэффициента автокорреляции, который может рассчитываться не только между соседними уровнями, т.е. сдвинутыми на один период, но и сдвинутыми на любое число единиц времени (L). Этот сдвиг, именуемый временным лагом, определяет и порядок коэффициентов автокорреляции: первого порядка (при L = 1), второго порядка (при L = 2) и т.д.. Однако наибольший интерес для исследования представляет вычисление нециклического коэффициента первого порядка, т.к. наиболее сильные искажения результатов анализа возникают при корреляции между исходными уровнями ряда 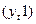 и теми же уровнями, сдвинутыми на одну единицу времени, т.е.
и теми же уровнями, сдвинутыми на одну единицу времени, т.е. 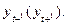
Тогда формулу коэффициента автокорреляции можно записать следующим образом:
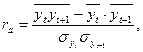
где 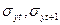 - среднее квадратическое отклонение рядов
- среднее квадратическое отклонение рядов  и
и 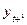 .
.
Для расчета коэффициента автокорреляции в Excel можно воспользоваться функцией КОРРЕЛ. Предположим, что базовая переменная включает диапазон ячеек А1:А15. Тогда коэффициент автокорреляции равен:
=КОРРЕЛ(А1:А14;А2:А15).
Автокорреляция ошибок, или автокорреляция в отклонениях от регрессионной модели. Одним из основных предпологаемых свойств отклонений 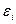 от регрессионной модели является их статистическая независимость между собой. Поскольку значения
от регрессионной модели является их статистическая независимость между собой. Поскольку значения 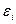 остаются неизвестными, то проверяется статистическая независимость их аналогов – отклонение
остаются неизвестными, то проверяется статистическая независимость их аналогов – отклонение 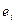 . При этом проверяется некоррелированность сдвинутыми на период величинами
. При этом проверяется некоррелированность сдвинутыми на период величинами 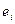 . Сдвиг производится во времени в случае временных рядов или по возрастанию переменной в случае перекрестных выборок. Для этих величин можно рассчитать коэффициент автокорреляции первого порядка (выборочный коэффициент корреляции между
. Сдвиг производится во времени в случае временных рядов или по возрастанию переменной в случае перекрестных выборок. Для этих величин можно рассчитать коэффициент автокорреляции первого порядка (выборочный коэффициент корреляции между 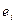 и
и 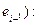
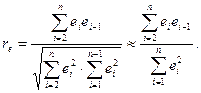
На практике, однако, в качестве теста используют тесно связанную с коэффициентом автокорреляции 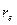 статистику Дарбина-Уотсона (Durbin-Watson). Тест Дарбина-Уотсона (DW) на наличие или отсутствие автокорреляции ошибок рассчитывается по формуле:
статистику Дарбина-Уотсона (Durbin-Watson). Тест Дарбина-Уотсона (DW) на наличие или отсутствие автокорреляции ошибок рассчитывается по формуле:

Нулевая гипотеза состоит в отсутствии автокорреляции автокорреляции:
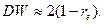
Содержательный смысл теста Дарбина-Уотсона заключается в следующем. Если между 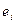 и
и 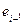 имеется достаточно высокая корреляция, то
имеется достаточно высокая корреляция, то  и
и 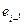 близки друг к другу и величина статистики DW мала. Это согласуется с последним выражением: если коэффициент
близки друг к другу и величина статистики DW мала. Это согласуется с последним выражением: если коэффициент 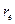 близок к единице, то величина DW близка к 2. Другой крайний случай возникает, когда точки наблюдений поочередно отклоняются в разные стороны от линий регрессии, и каждое последующее отклонение
близок к единице, то величина DW близка к 2. Другой крайний случай возникает, когда точки наблюдений поочередно отклоняются в разные стороны от линий регрессии, и каждое последующее отклонение 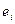 имеет, как правило, знак, противоположный предыдущему отклонению
имеет, как правило, знак, противоположный предыдущему отклонению 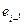 , т.е.
, т.е. 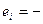
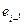 . В этом случае (
. В этом случае (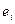 -
- 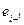 )
) 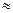
 и DW = 4. Это случай отрицательной автокорреляции остатков первого порядка. Во всех других случаях
и DW = 4. Это случай отрицательной автокорреляции остатков первого порядка. Во всех других случаях
0 < DW < 4.
Если бы распределение статистики DW было известно, то для проверки нулевой гипотезы об отсутствии автокорреляции можно было бы для заданного уровня значимости найти такое критическое значение 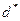 , что если DW > d
, что если DW > d 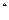 , то нулевая гипотеза
, то нулевая гипотеза  принимается, в противном случае она отвергается в пользу наличия автокорреляции. Однако проблема состоит в том, что распределение DW зависит не только от числа наблюдений n и количества регрессов m, но и от всей матрицы Х, и значит практическое применение этой процедуры затруднительно. Тем не менее, Дарбин и Уотсон доказали, что существует две границы, обычно обозначаемые
принимается, в противном случае она отвергается в пользу наличия автокорреляции. Однако проблема состоит в том, что распределение DW зависит не только от числа наблюдений n и количества регрессов m, но и от всей матрицы Х, и значит практическое применение этой процедуры затруднительно. Тем не менее, Дарбин и Уотсон доказали, что существует две границы, обычно обозначаемые 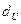 и
и 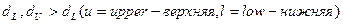 , которые зависят лишь от n, k и уровня значимости (и, следовательно, могут быть затабулированы) и обладают следующим свойством: если
, которые зависят лишь от n, k и уровня значимости (и, следовательно, могут быть затабулированы) и обладают следующим свойством: если 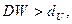 то
то 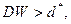 и значит, нулевая гипотеза отвергается в пользу альтернативной (табл.9). в случае
и значит, нулевая гипотеза отвергается в пользу альтернативной (табл.9). в случае 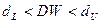 ситуация неопределенна, т.е. нельзя высказываться в пользу той или иной гипотезы.
ситуация неопределенна, т.е. нельзя высказываться в пользу той или иной гипотезы.
Проблему оценки в модели с авторегрессией рассмотрим на основе процедуры Кохрейна-Оркатта.
Начальным шагом этой процедуры является применение обычного метода наименьших квадратов к исходной системе и получение соответствующих остатков 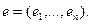
В качестве приближенного значения 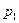 берется его МНК-оценка в регрессии:
берется его МНК-оценка в регрессии:
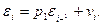
Проводится преобразование при 
 (36)
(36)
и находится МНК – оценки вектора параметров регрессии 
Строится новый вектор остатков:
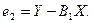
Процедура повторяется сначала, т.е. носит итерационный характер. Процесс обычно заканчивается, когда очередное приближение p отличается от предыдущего.
Процедура Дарбина. Перепишем уравнение (36) в виде:
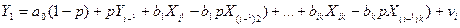
То есть 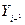 включается в число регрессоров, а p – в число оцениваемых параметров. Для этой системы определяются обычные МНК – оценки параметров
включается в число регрессоров, а p – в число оцениваемых параметров. Для этой системы определяются обычные МНК – оценки параметров 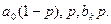 Оценки параметров
Оценки параметров  и p. Полученные оценки подставляются в уравнение (36) и находятся новые МНК – оценки параметров.
и p. Полученные оценки подставляются в уравнение (36) и находятся новые МНК – оценки параметров.
В случае когда после применения процедуры авторегрессионного преобразования остатки автокоррелированы, применяется авторегрессионное преобразование более высокого порядка. Так, для авторегрессионного процесса второго порядка ошибки удовлетворяют соотношению:
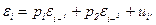
Однако часто истинной причиной первоначальной автокорреляции остатков может быть нелинейность формулы или неучтенный фактор. Данное обстоятельство является содержательным ограничением для применения авторегрессионного преобразования.
Кроме авторегрессионного преобразования, для устранения автокорреляции остатков и уточнения формулы регрессионной зависимости может использоваться метод скользящих средних (Moving Averages,или MA). В этом случае считается, что отклонения от линий регрессии 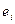 можно выразить как скользящие средние случайных нормально распределенных ошибок
можно выразить как скользящие средние случайных нормально распределенных ошибок 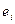 :
:
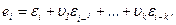
Это формула для преобразования МА k-го порядка. Для преобразования первого порядка формула имеет вид:
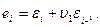
Параметры 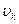 , как и в случае авторегресионного преобразования (АR) и метода скользящих средних (МА) позволяет проблему автокоррелиции остатков даже при небольших порядках.
, как и в случае авторегресионного преобразования (АR) и метода скользящих средних (МА) позволяет проблему автокоррелиции остатков даже при небольших порядках.
Методы АR и МА могут использоваться в сочетании с переходом от объемных величин в модели к приростным, для которых статистическая взаимосвязь может быть более точной и явной. Модель, сочетающая все эти подходы, назывется моделью ARIMA
(Autoregressive Integrated Moving Averages).
Преобразования АR, МА и модель ARIMA полезно использовать в тех случаях, когда уже ясен круг объясняющих переменных и общий вид оцениваемой формулы, но в то же время остается существенная автокорреляция остатков. Примером таких функций являются производственные функции, где объясняющими переменными служат используемые объемы или темпы прироста труда и капитала, а требуемой формулой является производственная функция Кобба-Дугласа, или CES.
Основная литература:1[ 200-225]
Дополнительная литература: 3[139-153].
Контрольные вопросы:
1.Дайте определение такому явлению как мультиколлинеарность
2.Какие меры можно предпринять для устранения мультиколлинеарности.
3. Как определить качество оценивания.
4.Оцените регрессионную зависимость у от х1 и х2.
5.Когда можно обнаружить гетероскедастичность?
6. Для чего проводят тест на гетероскедастичность.
7. Что означает эффективная оценка.
8. Причины возникновения автокорреляции.
9.При каких условиях возникает явление автокорреляции?
10.В чем заключается разница между положительной автокорреляцией и отрицательной автокорреляцией?
11.Какие методы используете при автокорреляции.
12.В чем заключается метод Дарбина-Уотсона
Тема лекции 7. Моделирование динамических процессов. Модели с распределенными лагами.Временные ряды.
Конспект лекции: Лаговая переменная -это переменная, влияние которой характеризуется некоторым запаздыванием. До сих пор мы считали, что на текущее значение зависимой переменной влияют только текущие значения объясняющих переменных. Такое предположение делается, когда мы пользуемся перекрестными данными (статистическими данными, относящимся к различным отраслям экономики, к различным фирмам и т.д.), где выборка берется из совокупности индивидов, фирм, стран и т.п. в соответствии с теми или иными условиями на какой – то один момент времени. Однако при использовании данными временного ряда мы можем ослабить это условие и исследовать, в какой степени запаздывает рассматриваемое влияние. Технический это известно как лаговая структура зависимости (структура с запаздыванием).
Например, если нас интересует исследование соотношения между расходами на жилье (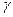 ), располагаемым личным доходом (
), располагаемым личным доходом (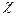 ), и индексом реальных цен на жилье (
), и индексом реальных цен на жилье (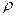 ) и если мы допустим, что логарифмическая регрессия является более подходящей, чем линейная, то мы можем построить регрессию:
) и если мы допустим, что логарифмическая регрессия является более подходящей, чем линейная, то мы можем построить регрессию:
 (37)
(37)
индекс t добавлен здесь е переменным для того, чтобы показать, что мы связываем текущие расходы на жилье с текущим доходом. Воспользовавшись данными за 1959 – 1983 гг. из приложения, мы получим:
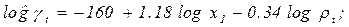
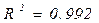 (38)
(38)
(с.о) (1,75) (0,05) (0,31)
В соответствии с данной регрессией расходы на жилье имеют положительную эластичность по доходам, близкую к единице, и отрицательную эластичность по цене, что и следовало ожидать.
Другой исследователь может предположить, что люди более склонны соотносить свои расходы на жилье не с текущими доходами и ценами, а с предшествующими, например, с прошлогодними доходами и ценами, которые мы обозначим 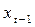 и
и 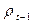 соответственно:
соответственно:
 (39)
(39)
Можно утверждать, что расходы на жилье подтверждены инерции и медленно согласуется с изменениями доходов и цен. В таблице 11 приведены данные по 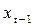 и
и 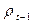 . Нужно просто сдвинуть данные для
. Нужно просто сдвинуть данные для 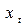 и
и 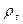 на один уровень ниже таблицы.
на один уровень ниже таблицы.
В 1980 г. Доход составлял 1021,6. по отношению к 1980 г. Эта сумма становится прошлогодним доходом, то есть 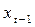 . То же происходит и оп отношению к другим годам. Точно так же индекс цен в 1980 г. Равнялся 93,0, а в 1981 г. он становится значением
. То же происходит и оп отношению к другим годам. Точно так же индекс цен в 1980 г. Равнялся 93,0, а в 1981 г. он становится значением 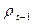 и т.д. Мы сталкиваемся с проблемой наблюдения величин
и т.д. Мы сталкиваемся с проблемой наблюдения величин 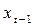 и
и 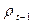 применительно к 1959г. Они равны величинам
применительно к 1959г. Они равны величинам 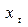 и
и 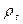 1958 г., мы должны либо отдельно найти значения этих величин, либо ограничивать период выборки 1960 – 1983 гг. здесь мы выбрали первый способ действий.
1958 г., мы должны либо отдельно найти значения этих величин, либо ограничивать период выборки 1960 – 1983 гг. здесь мы выбрали первый способ действий.
Оценив регрессионную зависимость 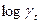 от
от 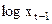 и
и 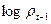 , получим:
, получим:
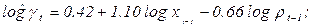
 (40)
(40)
(с.о) (1,74) (0,05) (0,31)
Первоначальный является регрессия между 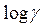 и текущими величинами
и текущими величинами 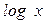 и
и 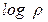 , взятыми с запаздыванием на один период.
, взятыми с запаздыванием на один период.
Естественно, что ничто не может помешать вам оценить регрессию между 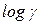 и величинами
и величинами  и
и  , взятыми с запаздыванием на два периода. Величина
, взятыми с запаздыванием на два периода. Величина 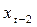 в 1982 г. – та же что
в 1982 г. – та же что  в 1980г., и т.д. Данные для
в 1980г., и т.д. Данные для 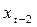 и
и 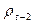 показаны в пятой и восьмой колонках табл. 6.9. оценив регрессивную зависимость
показаны в пятой и восьмой колонках табл. 6.9. оценив регрессивную зависимость 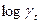 от
от 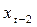 и
и 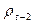 , получим:
, получим:
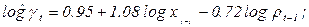
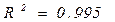 (41)
(41)
(с.о) (1,77) (0,05) (0,31)
В общем если какая – то переменная появляется в модели с запаздыванием на S периодов, тона записывается с нижним индексом (t - s).Одна и та же переменная может в данном уравнении появляться несколько раз с разными запаздываниями. Например, при анализе функции спроса на жилье было бы разумным выдвинуть гипотезу, что текущий доход, прошлогодний доход и, возможна, доход на несколько предыдущих лет, вместе взятые, влияют на текущие расходы на жилье. Спецификация запаздываний применительно к переменным в модели называется лаговой структурой (структурой с запаздыванием); она может являться важным аспектом модели и выступать в качестве спецификации самих переменных.
Например, нас интересует исследование соотношения между расходами на жилье (у), располагаемым личным доходом (х), и индексом реальных цен на жилье (р) и если мы допустим, что логарифмическая регрессия является более подходящей, чем линейная, то мы можем построить регрессию:
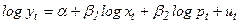
индекс t добавлен здесь к переменным для того, чтобы показать, что мы связываем текущие расходы на жилье с текущим доходом. Воспользовавшись данными за 1959-1983гг. из приложения, мы получим:
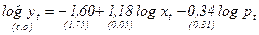 ,
, 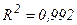 .
.
В соответствии с данной регрессией расходы на жилье имеют положительную эластичность по доходам, близкую к единице, и отрицательную эластичность по цене, что и следовало ожидать.
Другой исследователь может предположить, что люди более склонны соотносить свои расходы на жилье не с текущими доходами и ценами, а с предшествующими, например с прошлогодними доходом и ценами, которые мы обозначим  и
и  соответственно:
соответственно:
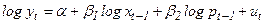
Можно утверждать, что расходы на жилье подвержены инерции и медленно согласуются с изменениями доходов и цен. Для того чтобы получить данные для хt-1 и pt-1, нужно просто сдвинуть данные для хt и pt на один уровень ниже в таблице.
Модель считается динамической, если она включает в себя значения переменных не только для текущего, но и для предыдущих моментов времени. Число периодов, на которое запаздывает воздействие фактора на текущее состояние процесса, называется лагом.
Например, темп инфляции pi зависит от предложения денег в текущем и предшествующих периодах времени:
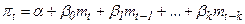
Здесь b0 – краткосрочный коэффициент, определяющий влияние темпа предложения денег mi в текущем периоде. Величина 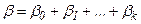 представляет собой долгосрочный коэффициент. Если темп предложения денег m в каждом периоде j возрастает на единицу, то темп инфляции в периоде t возрастает на b единиц.
представляет собой долгосрочный коэффициент. Если темп предложения денег m в каждом периоде j возрастает на единицу, то темп инфляции в периоде t возрастает на b единиц.
Укажем причины возникновения лагов.
Психологические. Люди не могут изменить свои предложения немедленно вслед за изменением цен или дохода. В течение нескольких периодов они привыкают к новым условиям.
Технологические. Если цена капитала снизится, это не отразится немедленно на объеме выпуска фирмы.
Институциональные. Контракты найма на работу заключаются на определенный срок. Облигации погашаются через несколько лет.
Модель с распределенным лагом имеет вид:
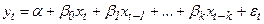
где 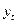 -зависимая переменная,
-зависимая переменная,  -объясняющая переменная с лагом i периодов
-объясняющая переменная с лагом i периодов
Авторегрессионная модель:
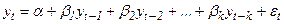
Авторегрессионная модель с распределенным лагом, например, 
Модели с распределенными лагами
Формально метод наименьших квадратов можно применить к модели с распределенным лагом. Переменные 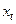 ,
,  ,
,  ,… последовательно включаются в уравнение регрессии, пока оцененные коэффициенты не станут статистически незначимыми, или хотя бы один из них не поменяет знак. Однако, этот способ имеет существенный недостаток вследствие возникновения мультиколлинеарности из-за коррелированности
,… последовательно включаются в уравнение регрессии, пока оцененные коэффициенты не станут статистически незначимыми, или хотя бы один из них не поменяет знак. Однако, этот способ имеет существенный недостаток вследствие возникновения мультиколлинеарности из-за коррелированности 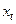 ,
, 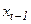 ,
,  ,
,
В методе Койка делается предложение, что коэффициенты 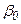
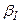 , … убывают в геометрической прогрессии:
, … убывают в геометрической прогрессии:  ,
, 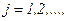
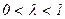 .
.
и модель принимает вид
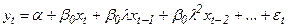 (42)
(42)
Выполняется следующее преобразование: запишем (42) для момента времени t-1:
 (43)
(43)
Умножим (43) на l и вычтем из (42):
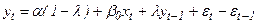
Здесь оцениваемые параметры. Можно использовать МНК. Однако, нарушено 4-е условие Гаусса-Маркова: объясняющая переменная  коррелированна со случайным членом
коррелированна со случайным членом  . Вследствие этого не обеспечивается несмещенность и состоятельность оценок коэффициентов.
. Вследствие этого не обеспечивается несмещенность и состоятельность оценок коэффициентов.
Коэффициенты 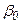 ,
, 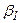 ,
, 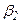 , … необязательно должны монотонно убывать. Они могут возрастать, затем убы
, … необязательно должны монотонно убывать. Они могут возрастать, затем убы
|
|
 2020-01-15
2020-01-15 366
366








