Комплексное число 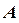 можно представить в таком виде:
можно представить в таком виде:
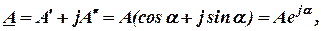 (3.7)
(3.7)
где 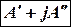 - алгебраическая форма;
- алгебраическая форма;
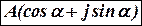 - тригонометрическая форма;
- тригонометрическая форма;
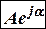 - показательная форма.
- показательная форма.
Здесь: 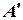 - действительная часть комплексного числа;
- действительная часть комплексного числа; 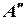 - мнимая часть комплексного числа;
- мнимая часть комплексного числа; 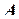 - модуль комплексного числа;
- модуль комплексного числа; 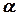 - аргумент комплексного числа;
- аргумент комплексного числа; 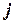 - мнимая единица (
- мнимая единица (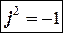 ).
).
Комплексное число может быть изображено на комплексной плоскости в виде радиус-вектора 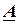 , который соединяет начало координат с точкой
, который соединяет начало координат с точкой 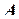 комплексного числа. Проекции радиус-вектора
комплексного числа. Проекции радиус-вектора 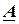 на действительную и мнимую координатные оси являются координатами комплексного числа, записанного в алгебраической или тригонометрической форме, а угол
на действительную и мнимую координатные оси являются координатами комплексного числа, записанного в алгебраической или тригонометрической форме, а угол 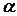 между радиус-вектором
между радиус-вектором 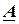 и действительной осью является его аргументом при записи в тригонометрической или показательной форме. Отсюда переход от алгебраической формы к показательной форме и наоборот:
и действительной осью является его аргументом при записи в тригонометрической или показательной форме. Отсюда переход от алгебраической формы к показательной форме и наоборот:

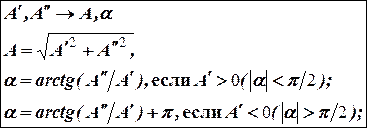
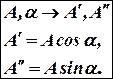
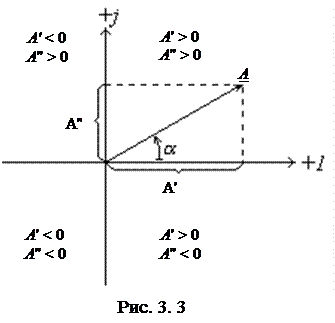
Комплексная плоскость с комплексным числом 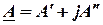 , знаки действительной и мнимой частей комплексного числа в четырех квадрантах показана на рис. 3.3. Действия над комплексными числами достаточно широко изучаются в курсе математики, потому ограничимся только выводами.
, знаки действительной и мнимой частей комплексного числа в четырех квадрантах показана на рис. 3.3. Действия над комплексными числами достаточно широко изучаются в курсе математики, потому ограничимся только выводами.
Для комплексных чисел, записанных в любой форме, могут применяться все основные математические действия, но сложение и вычитание лучше проводить в алгебраической форме, а умножение и деление - в показательной.
Чтобы сложить (вычесть) два комплексных числа в алгебраической форме
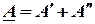 і
і 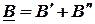 ,
,
необходимо сложить (вычесть) отдельно их действительные и мнимые части, т.е.:
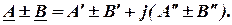
При умножении комплексных чисел в показательной форме
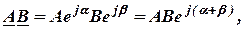
то есть их модули перемножают, а аргументы суммируют.
При делении комплексных чисел в показательной форме их модули делят, а аргументы вычитают:

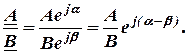
Запишем также наиболее распространенные соотношения, которые следуют из формулы Эйлера:


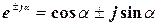 ;
; 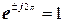 ;
; 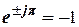 ;
; 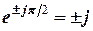 .
.
 2020-01-15
2020-01-15 168
168








