Электрическая цепь с последовательным соединением

R, L и C  элементов. Закон Ома в комплексной форме. 

Комплексное и полное сопротивление электрической цепи

 Если к участку с последовательным соединением R, L и С (рис. 3.4) элементов приложить синусоидальное напряжение , то ток в цепи тоже будет синусоидальным: . Заменяя мгновенные значения их комплексными выражениями, получим

.

Ранее (табл. 3.1) было получено:

; ; .

Поэтому

 . (3.12)

Вынося в выражении (3.12) ток 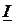 за скобки, получим:

 .             (3.13)

Введем обозначение

и назовем его комплексным сопротивлением. После подстановки  в выражение (3.13) получим закон Ома в комплексной форме:

.

Введем также                         

                                             (3.14)

и назовем его реактивным сопротивлением.

Представим  в показательной форме:

                                                               (3.15)

где                                                         (3.16)

- модуль комплексного сопротивления, который называется полным сопротивлением,

                                       (3.17)

- аргумент комплексного сопротивления.

Выразим  через  и , представив их в показательной форме:

                                (3.18)

Из (3.15) и (3.18) получаем:

Таким образом, угол сдвига фаз между напряжением и током равняется аргументу комплексного сопротивления (3.15).

 

Характер нагрузки участка

Знак угла сдвига фаз между током и напряжением определяется знаком реактивного сопротивления  (3.14, 3.17).

Если , то участок имеет активно-индуктивный характер, то есть ток по фазе отстает от напряжения на угол  

Если 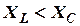, то участок имеет активно-емкостной характер, то есть ток по фазе опережает напряжение .

Когда , то  и имеет место режим резонанса, при котором сопротивление участка цепи активно.

Векторная диаграмма напряжений.