2020-01-15
95
R, L и C элементов
Пусть к цепи (рис. 3.6), которая состоит из параллельно соединенных R, L и C элементов, приложено напряжение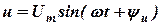 
. Введём для заданного синусоидального напряжения комплексное действующее напряжение, которое его изображает:
.
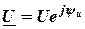Затем применим для каждой из ветвей закон Ома в комплексной форме. Получим:
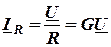; (3.19)
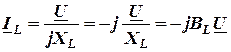; (3.20)
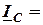
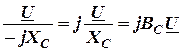. (3.21)
Для данной цепи запишем уравнение первого закона Кирхгофа в комплексной форме:
,
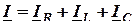и подставим в него полученные значения токов:
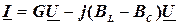. (3.22)
Обозначив разность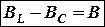 
(3.23)
и назвав ее реактивная проводимость, окончательно найдем
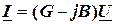. (3.24)
Величина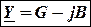 
(3.25)
называется комплексная проводимость электрической цепи и может быть записана в показательной форме
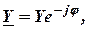(3.26)
где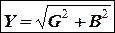 
(3.27)
является модулем комплексного числа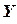 
, который представляет собой полную проводимость разветвлённой цепи, а величина
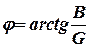(3.28)
- аргументом того же комплексного числа 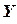, который определяет сдвиг фаз между напряжением 
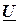и током 
.
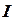Введение комплексной проводимости 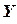позволяет найти ток в неразветвлённой части цепи:
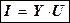. (3.29)
Последнее уравнение (3.29) представляет собой закон Ома для разветвлённой цепи в комплексной форме.
Векторная диаграмма токов. Треугольники токов,
Проводимостей и мощностей
После нахождения тока до разветвления можно построить векторную диаграмму токов вместе с вектором напряжения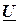 
, начальная фаза которого 
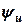чаще всего принимается равной нулю. От векторной диаграммы, переходя к модулям, получаем треугольник токов. Затем, разделив и умножив стороны треугольника тока на напряжение, получим треугольники проводимостей и мощностей (см. табл. 3.2).
