Точечные группы симметрии

 

Понятие класса симметрии кристалла эквивалентно понятию точечной группы симметрии для многогранника. Математическое определение группы: множество различных элементов составляют группу, если оно удовлетворяет следующим условиям:

1) произведение двух любых элементов или квадрат какого-либо элемента
множества принадлежит тому же множеству;

2) для любых трёх элементов множества выполняется ассоциативный за­
кон: а(bc) = (ab)c;

3) в множестве существует единичный элемент е такой, что ае = еа = а;

4) для любого элемента а существует элемент а^–1, принадлежащий тому же
множеству, так что аа^–1 = а^–1 а = е.

Всем этим условиям удовлетворяют 32 класса симметрии. Элементами множества здесь являются преобразования симметрии, а операцией «умножения» элементов группы – последовательное применение этих преобразований.

Например: 1) два последовательно проведённых симметричных преобразования эквивалентны третьему симметричному преобразованию (теоремы 1 и 5); 2) ко­нечный результат этих преобразований не зависит от очерёдности их проведе­ния (теоремы 2, 2а, 2b); 3) единичным элементом для любого класса симметрии можно считать поворот вокруг оси 1-го порядка.

   Таким образом, преобразования симметрии кристаллографического класса образуют математическую группу.

    Группа называется точечной, если симметричные преобразования кристаллического многогранника оставляют на месте по крайней мере одну его точку, в которой пересекаются все элементы симметрии. Кратностью точечной группы называется максимальное количество эквивалентных точек, которое можно получить из одной точки, преобразуя её всеми операциями симметрии, входящими в группу.

 

Кратность группы соответствует числу граней общей простой формы, характеризующей группу. Группа является подгруппой другой группы, если все элементы симметрии первой группы входят в состав элементов второй группы и если их множество само образует группу.

В каждой сингонии есть группа высшего порядка (один класс), так называемая голоэдрия. Все остальные классы этой сингонии называются мероэдрическими и составляют подгруппы голоэдрического класса.

Голоэдрия включает гемиэдрию, тетардоэдрию и огдоэдрию. Кратность мероэдрических классов по сравнению с кратностью голоэдрического класса: гемиэдрических классов в 2 раза меньше; тетардоэдрических классов в 4 раза меньше; огдоэдрических классов в 8 раз меньше кратности голоэдрического класса. Для примера рассмотрим кубическую сингонию. Голоэдрия (планаксиальный класс 3L₄4L₃6L₂9PC): группа – m3m; кратность – 48; общая простая форма – сорокавосьмигранник (48 граней). Гемиэндрия: группы – m3, 432; их соответствующая кратность – 24, 24; общая простая форма – дидодекаэдр (24 грани), пентагонтриоктаэдр (24 грани). Тетартоэдрия: группы – 3m, 23; кратность – 24, 12; общая простая форма – гексатетраэдр (24 грани), пента­гон додекаэдр (12 граней).

В настоящее время изучены структуры примерно 20 000 кристаллических веществ. Их распределение по сингониям и классам очень неравномерное. Чем проще структура, тем выше его симметрия. Для примера далее представлены несколько (из 32) классов и их представители.

1. Самый богатый класс 2/m (22 %) - (планаксиальный, моноклинная син): гипс, тальк, слюда, нафталин, бура.

2. Следующий по распространению класс m3m (19 %) –(планаксиальный, кубическая сингония): медь, серебро, золото, германий, кремний, алмаз и др.; ионные кристаллы; гранаты, шпинели и т. д.

3. Класс mmm (13 %) – (планаксиальный, ромбическая сингония): бензол, йод, топаз.

4. Класс 4/mmm (7 %) – (планаксиальный, тетрагональная сингония): ру­тил, белое олово.

5. Класс 222 (7 %) – (аксиальный, ромбическая сингония): сегнетовая соль, некоторые полупроводники.

6. Класс 1 (3 %) – (примитивный, триклинная сингония): медный купорос, кианит.

Формы кристаллов

Хотя все кристаллы одного и того же вещества должны иметь одно и то же сочетание элементов симметрии, это не означает, что облик всех кристаллов будет одинаковым. Гранат, обладающий такой же симметрией, как и простой куб (13 осей, 9 плоскостей и центр симметрии), часто встречается в виде кристаллов с 12 ромбическими гранями, т. е. в виде ромбододекаэдров (рис. 4.2).

Встречаются также тела кубической формы с 24 гранями – икоситетраэдры (трапецоэдры), и эти два вида кристаллов описываются как различные простые формы.

                                  

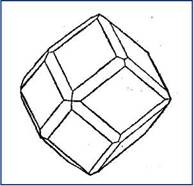
Рис. 4.2.Кристаллы граната с одной и двумя простыми формами

 

Простой идеальной формой кристалла называется многогранник, все грани которого можно получить из одной грани с помощью преобразований симметрии, свойственных точечной группе симметрии данного кристалла. Для всех граней простой формы идеального кристалла скорости роста одинаковы и все грани кристаллографически равны. Одна и та же простая форма может встретиться в нескольких классах симметрии. Примером служит куб в классах кубической сингонии. Простым формам с малым числом граней отвечают самые простые символы.

 

 

Простую форму определяют как совокупность симметрично эквивалентных плоскостей, получаемых из одной плоскости, если размножить её с помо­щью операций симметрии, свойственных данному классу симметрии. Простую форму также можно точно определить как «совокупность граней, отвечающую данной симметрии, если дана одна грань». Предположим, что вещество имеет структуру, которая создаёт гексагональную ось симметрии, нормальную к плоскости симметрии. Грань, наклонная как к оси, так и к плоскости, будет повторяться вокруг оси шесть раз. Эти шесть граней отразятся по другую сто­рону плоскости, так что в итоге образуется форма гексагональной бипирамиды (рис. 4.3).

 

                  

 

Рис. 4.3.Гексагональная бипирамида

 

Рассмотрим кристалл высшей категории класса m3m. В качестве исходной выберем грань (111) и размножим её всеми операциями этого класса: 3L₄4L36L₂9PC. Проведя все преобразования (повороты вокруг оси 4Z, отражения в плоскости симметрии, совпадающей с плоскостью чертежа), получим 8 граней, которые все одинаково наклонены к осям координат. В совокупности они образуют октаэдр (рис.4.4). Символы всех 8 граней объединяются одним значком: {111}.

 

       

                                                                                                         

          плоскость (111)

Рис. 4.4.Простая форма – октаэдр

 

Размножив грань (100), получим простую форму в виде куба, число граней которого равно 6:

{100 }: (100),(100),(010),(010),(001),(001).

   Размножив грань (110), получим простую форму в виде ромбического додекаэдра, число граней которого равно 12).

                                        

                                                                                     

 

 

    плоскость (100)                                             плоскость (110)

 

 

Каждый класс симметрии характеризуется соответствующими ему про­стыми формами. Вид простой формы и число её граней зависят от того, как расположены эти грани по отношению к элементам симметрии. Чем меньше число элементов симметрии, тем больше число симметрично повторяемых гра­ней получающегося многогранника.   

Если теперь задать грань в самом общем положении, где нет выходов никаких элементов симметрии, то в рассматриваемом классе m3m получим 48-гранник.

Простые формы кристалла могут быть частными и общими. Их различие объясняется расположением исходной грани по отношению к элементам симметрии. Частная простая форма кристалла получается, если исходная грань располагается параллельно или перпендикулярно осям или плоскостям симмет­рии кристалла или она образует одинаковые углы с двумя равными элементами симметрии.

 

Общая простая форма кристалла получается, если исходная грань задана произвольно в общем положении, т. е. не на элементах симметрии.

В каждом классе симметрии может быть одна общая форма и несколько частных форм (рис. 4.2). Число граней общей простой формы соответствует кратности точечной группы. Число граней частных простых форм соответствует кратностям её подгрупп.

Существует 47 простых форм кристаллов, из них 22 возможны для кристаллов средней и низшей категорий (рис. 4.5). К простым формам средней и низшей категорий относятся следующие формы: моноэдр (состоит из одной грани); пинакоид (состоит из двух параллельных граней); диэдр (состоит из двух непараллельных разных граней).

Рис. 4.5. Простые формы кристаллов средней и низшей категорий

 

Следующие более сложные формы – пирамиды, призмы; дипирамиды и дипризмы. Если они тригональные, то в их основании лежит равносторонний треугольник. Если они тетрагональные, то в основании лежит квадрат. В случае гексагональных призм в основании лежит правильный шести­угольник.

Возможны ещё четыре простые формы:

1) тетраэдр (замкнутый четырёхгранник: грани – равнобедренные тре­угольники);

2) трапецоэдр (тригональный, гексагональный, тетрагональный; грани – четырёхугольники с двумя равными смежными сторонами);

3) ромбоэдр (вытянутый или сжатый куб: грани имеют форму ромбов);
    4) скаленоэдр (тетрагональный и тригональный: грани имеют форму не­равносторонних треугольников).

Простые формы могут быть открытыми и закрытыми. Открытые формы не замыкают пространство и могут существовать лишь с другими формами. Среди них: моноэдр, диэдр, пинакоид, призмы, дипризмы, пирамиды. Закрытые формы полностью замыкают пространство. Среди них: тетраэдр, дипирамида, трапецоэдр, ромбоэдр, скаленоэдр

Простые формы высшей категории тетраэдр, октаэдр, куб являются закрытыми. Остальные простые формы кубической сингонии можно получить из этих, удваивая, утраивая, учетверяя и ушестеряя число их граней. У тетраэдра кубической сингонии грани – равносторонние треугольники.

   Надстраивая на гранях тетраэдра по:

3 треугольника, получим тригонтритетраэдр;

3 четырёхугольника, получим тетрагонтритетраэдр;

3 пятиугольника, получим пентагонтритетраэдр;

6 треугольников, получим гексатетраэдр.

   Из октаэдра получают: тригонтриоктаэдр, тетрагонтриоктаэдр, пентагонтриоктаэдр, гексагонтриоктаэдр (48-гранник).

Из куба получают: тетрагексаэдр; ромбический додекаэдр.