Примеры оценивания выполнения заданий C4

 

Пример 1.1. Решение задачи 1, комментарий и оценка этого решения.

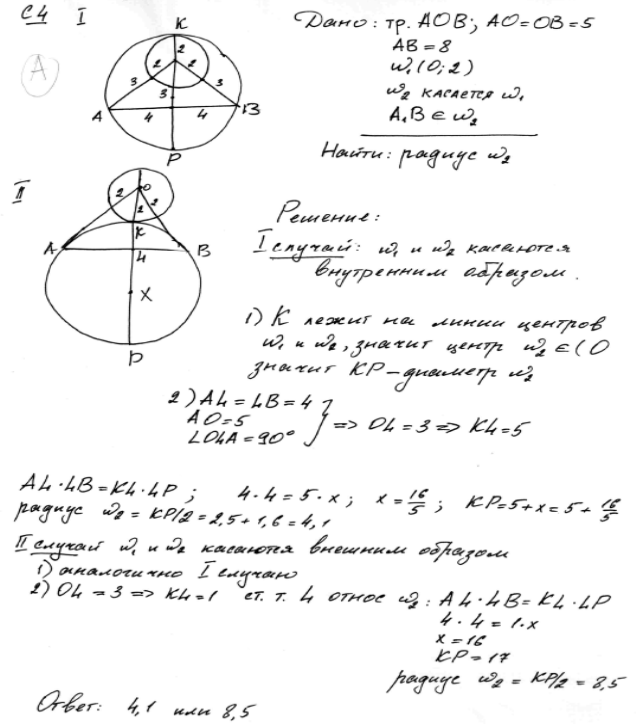
Комментарий.

 

В предложенном решении реализованы все геометрические конфигурации.

Получен верный ответ.

Формально, нет описания точки L и она не указана на первом рисунке. Но зато – указана на втором рисунке.

Решение оценивается максимальным баллом.

 

Оценка эксперта: 3 балла.

Пример 1.2. Решение задачи 1, комментарий и оценка этого решения.

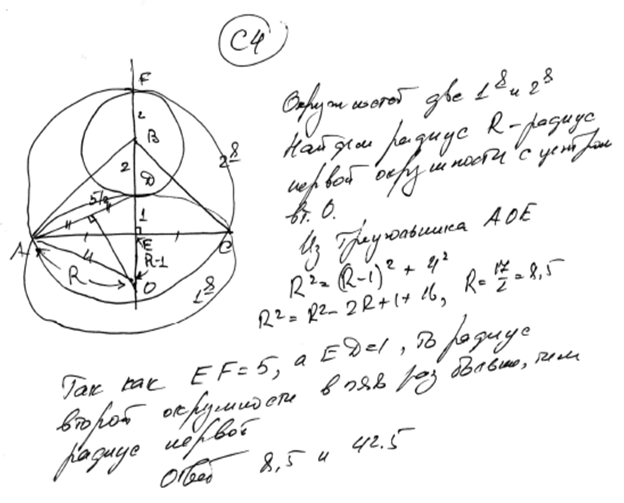
Комментарий.

 

В решении рассмотрены все возможные геометрические конфигурации.

Правильно найден радиус одной окружности, а радиус второй находится из неверного предположения: радиус второй окружности в 5 раз больше радиуса первой. Ясно, что тут нельзя поставить 3 балла, как нельзя и поставить 0 баллов.

Конечно, предположение о пятикратном увеличении радиуса удивительно несуразно и, честно говоря, безумно. Из неких общих соображений и привычек, следовало бы за это при проверке серьезно «наказать» автора, т.е. поставить 1 балл.

Однако, по приведенным критериям это решение следует оценить в 2 балла. По мнению разработчиков КИМ ЕГЭ-2010, в первую очередь, оцениваются успехи и положительные результаты выпускника, а при дальнейших ошибках возможна «амнистия».

Оценка эксперта: 2 балла.

 

Пример 1.3. Решение задачи 1, комментарий и оценка этого решения.

Комментарий.

Сложный случай. Рассмотрены и верно описаны все геометрические конфигурации. Для каждой из них верно найдены необходимые тригонометрические величины.

Но, оба раза – одна и та же ошибка в вычислении радиуса, а именно, в теореме синусов «забыта» сторона, на которую опирается вписанный угол. Оба радиуса найдены в итоге неверно и поэтому 2 балла по приведенным критериям выставить невозможно. Более того, если абсолютно строго придерживаться критериев, то поставить и 1 балл нельзя: ученик сделал, формально, не арифметическую ошибку.

Однако, оценить это решение в 0 баллов недопустимо: ведь автор для обеих конфигураций практически верно разобрал все геометрические детали и (дважды) ошибся лишь в заключительном шаге.

Оценка эксперта: 1 балл.

Пример 1.4. Решение задачи 1, комментарий и оценка этого решения.

Комментарий.

 

В решении рассмотрена только одна из двух геометрических конфигураций. Для случая внешнего касания окружностей задача решена верно.

Авторское указание двух случаев относится к двум способам решения задачи для одного и того же способа расположения окружностей.

Оценка эксперта: 2 балла.

       Рассмотрим еще одну планиметрическую задачу уровня сложности С4 и примеры оценивания ее выполнения.

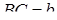Задача 2.  В параллелограмме  известны стороны ,  и угол . Найдите расстояние между центрами окружностей, описанных около треугольников  и .

Решение №1.

Треугольники  расположены в разных полуплоскостях относительно прямой . Поэтому также по разные стороны от нее расположены и центры 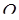 и  описанных около них окружностей, лежащие на серединном перпендикуляре  к их общей стороне , следовательно, , где  — середина .

Возможны три случая:

1. ,

тогда 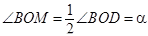 (теорема о вписанном угле),

2. ,

 

тогда    (теорема о вписанном угле),

3. , тогда точк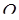и  и  совпадают.

 

Во всех рассмотренных случаях имеем

.

Найдем :

а)  (теорема косинусов для ),

б) ,

в) .

Ответ: .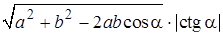

Решение №2.

Треугольник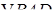и  и  симметричны относительно точки – середины . Поэтому при любом расположении центров  и  окружностей (; см. рисунки) искомое расстояние  в два раза больше, чем расстояние от точки  до , т.е. .

Из прямоугольного треугольник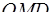а : .

, а  находим из теоремы косинусов, применённой к треугольнику : .

 – радиус окружности, который находим по теореме синусов, применённой к треугольнику : .

В итоге, .

 

Ответ: .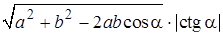

Комментарий.

Эта задача — по планиметрии. В ней требуется найти расстояние между некоторыми точками в заданной геометрической фигуре.

Задача не очень проста по следующим причинам:

· для вычисления искомого расстояния используются некоторые хотя и стандартные, но не слишком часто употребляемые в задачах факты, такие как местонахождение центра описанной окружности, соотношение между вписанным и центральным углами, еорема синусов (для нахождения радиусов окружности);

· условие задачи, ввиду недостаточной определенности данного в ней угла, не совсем однозначно задает расположение центров, между которыми ищется расстояние, — они могут лежать как внутри соответствующих треугольников, так и снаружи, или даже на их границе, от чего могут зависеть (см. решение №1) рассуждения, необходимые для решения задачи;

· возможно решение (см. решение №2), в котором различные конфигурации аналитически описываются одинаково: расстояние между центрами в два раза больше, чем расстояние от одного из них до диагонали, относительно которой центры симметричны, а расстояние до диагонали ищется из прямоугольного треугольника с гипотенузой, равной радиусу, и катетом, равным половине диагонали, – такая аналитика автоматически даёт модуль котангенса.

При любом подходе к решению этой задачи от выпускника требуется понимание реализуемости различных геометрических конфигураций и умение вычислять стандартные элементы в заданном треугольнике.

Отметим, что в обоих решениях имеется доказательство равенства  (в решении №1 – несколько менее обоснованное). Однако, для учащихся при выполнении заданий С4 на ЕГЭ считается допустимым предъявление этого равенства и без подробных обоснований.

Критерии оценивания остаются такими же, как и в задаче 1.