Основные свойства графа группы

Наши примеры графов различных групп имеют некоторые общие существенные свойства.

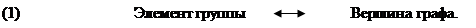
Элементы группы находятся во взаимно однозначном соответствии с вершинами графа. Каждая вершина графа соответствует в точности одному элементу группы, и наоборот.

Каждое ребро графической сети есть направленный отрезок, и отрезки одного «цвета» связаны с одной и той же образующей группы. Движение, начинающееся в некоторой вершине, вдоль отрезка в направлении, указанном стрелкой, соответствует умножению справа на связанный с этим отрезком образующий элемент (назовем его а), в то время как движение вдоль отрезка в направлении, противоположном указанному стрелкой, соответствует умножению справа на а ^–1 — элемент, обратный к образующей. Например, если А, В и С на рис. 2.2.1 суть вершины графа, соответствующие элементам х, y и z некоторой группы соответственно, то движение от В к С отвечает умножению элемента у на а, так что уа ^–1= z, а движение от В к A отвечает умножению элемента у на а ^–1, т.е. у а ^–1 = х.

 

Каждое слово, представляющее элемент группы, можно интерпретировать как путь, или некоторую последовательность направленных отрезков графа, и наоборот. В каждой вершине пути, соответствующего некоторому слову, очередное движение определяется следующим сомножителем в слове. Так как любой сомножитель — это или одна из образующих, или элемент, обратный к образующей, то каждая вершина является концевой точкой двух направленных отрезков одинакового «цвета» — одного, направленного к вершине, и другого, направленного от нее. Если группа имеет две образующие, а и b, то в каждой вершине сходятся четыре ребра, так как четыре элемента a, a ^–1, b, b ^–l соответствуют четырем возможным движениям, начинающимся в этой вершине. Вообще в каждой вершине есть одно «входящее» и одно «исходящее» ребро для каждой образующей.

 

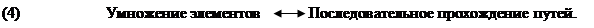
Умножение двух элементов группы соответствует прохождению на графе пути, составленного из двух последовательных путей. Произведение rs = t элементов r и s группы можно интерпретировать как путь в графе, который строится следующим образом. Запишем r и s как слова от образующих и их обратных. Выходя из вершины, соответствующей элементу I, пройдем путь, описанный словом, определенным элементом r. Конечная точка этого пути соответствует элементу r. Теперь, принимая за начальную точку r -вершину[23] (т.е. вершину, соответствующую элементу r), пройдем путь, описанный словом, соответствующим элементу s. Этот путь закончится в вершине, соответствующей элементу t = rs, вне зависимости от того, какие слова используются для представления элементов r и s.

 

Любое слово, представляющее элемент I, соответствует замкнутому пути на графе. Предположим, что W — слово, представляющее элемент I. Например, в группе самосовмещений равностороннего треугольника за W можно взять frfr. Если принять вершину, соответствующую элементу I, за начальную точку, то путь, определяемый словом W, окончится в I -вершине. Мы называем путь замкнутым, если его начальная и конечная точки совпадают. Если за начальную точку взята вершина, соответствующая элементу t, отличному от I, то путь, заданный словом W, окончится в t -вершине, так как tW — t. Таким образом, если W — слово, представляющее элемент I, то путь, определяемый этим словом, будет замкнутым вне зависимости от того, какая точка принята за начальную. Таким образом, граф группы обладает некоторым свойством однородности.[24] (Произвольный граф называется однородным степени n если в каждую его вершину входит и из каждой его вершины выходит одинаковое число направленных отрезков, равное n. Граф группы будет однородным графом в этом смысле). Из этого свойства графа группы следует, что его вершины можно пометить так, чтобы любая наперед заданная вершина соответствовала элементу I. <…>

 

Граф группы является связной сетью, т.е. существует путь из любой вершины в любую другую вершину. Если r и s — два произвольных элемента группы, то существует элемент х = r ^–l s, такой, что rx = s <…>. Ясно, что если W — произвольное слово, представляющее элемент х = r ^–1 s, то rW = s; таким образом, если вершина, соответствующая элементу r, взята за начальную точку, то путь, описанный словом W, ведет от r -вершины к s -вершине.

Теперь выпишем вместе все соответствия, установленные в ходе предыдущих рассуждений:

 

Группа	Граф
Элемент	Вершина
Образующая	Направленные ребра одного «цвета»
Слово	Путь
Умножение элементов	Последовательное прохождение путей
Слово, представляющее элемент I	Замкнутый путь
Разрешимость уравнения rx = s	Сеть связна

 

Таким образом, конкретная группа может быть определена при помощи графической схемы (сети), составленной из направленных отрезков и обладающей основными свойствами, которыми (как мы установили) должен обладать граф группы. Внутренней структурой такой сети группа вполне определяется, т.к. нам известно, каким образом последовательному прохождению путей должно соответствовать умножение элементов группы.[25] А из приведенных выше соответствий видно, что образующая в группе соответствует направленным ребрам одного «цвета» в графе, а каждый элемент группы соответствует вершинам в графе.

ЛИТЕРАТУРА

1. Введение в теорию групп / П. С. Александров — М.: Издательство «Наука», 1980. — С. 144.

2. Группы и их графы / И. Гроссман, В. Магнус; под ред. В. Е. Тараканова — М.: Издательство «Мир», 1971. — С. 245.

3. Курс алгебры / Э. Б. Винберг— 2-е изд., испр. и доп. М.: Изд-во «Факториал Пресс», 2001— С. 544.

4. Лекции по математике. Т. 8 / Теория групп: учебн. пособие / В. Босс — М.: КомКнига, 2007. — С. 216.

5. Линейная алгебра и некоторые приложения / Л. И. Головина. — 3-е изд., перераб. и доп. — М.: Издательство «Наука», 1979. — С. 392.

6. Основы теории групп / М. И. Каргаполов, Ю. И. Мерзляков. — 3-е изд., перераб. и доп.— М.: Наука, 1982.— С. 288.

7. Теория групп / А. Г. Курош. — М.: Издательство «Наука», 1967. — С. 648.

8. Группа (математика) // Википедия / Свободная энциклопедия [Электронный ресурс]. ¾ Режим доступа: http://ru.wikipedia.org

[1] Множество М с одной бинарной алгебраической операцией принято теперь называть группоидом.

 

[2] Теория групп / А. Г. Курош. — М.: Издательство «Наука», 1967. — С. 16–17.

[3] Линейная алгебра и некоторые приложения / Л. И. Головина. — 3-е изд., перераб. и доп. — М.: Издательство «Наука», 1979. — С. 274–276.

[4] Группа (математика) // Википедия / Свободная энциклопедия [Электронный ресурс]. ¾ Режим доступа: http://ru.wikipedia.org

[5] Линейная алгебра и некоторые приложения / Л. И. Головина. — 3-е изд., перераб. и доп. — М.: Издательство «Наука», 1979. — С. 272–275.

[6] Группы и их графы / И. Гроссман, В. Магнус; под ред. В. Е. Тараканова — М.: Издательство «Мир», 1971. — С. 78.

[7] Группы и их графы / И. Гроссман, В. Магнус; под ред. В. Е. Тараканова — М.: Издательство «Мир», 1971. — С. 78.

[8] Тот же

[9] Группы и их графы / И. Гроссман, В. Магнус; под ред. В. Е. Тараканова — М.: Издательство «Мир», 1971. — С. 59–61.

[10] Введение в теорию групп / П. С. Александров — М.: Издательство «Наука», 1980. — С. 61.

[11] Введение в теорию групп / П. С. Александров — М.: Издательство «Наука», 1980. — С. 62.

[12] Теория групп / А. Г. Курош. — М.: Издательство «Наука», 1967. — С. 43–44.

[13]Лекции по математике. Т. 8 / Теория групп: учебн. пособие / В. Босс — М.: КомКнига, 2007. — С. 107.

[14] Транспозиция — операция перемещения двух элементов перестановки.

[15] Элементарной матрицей называется матрица, полученная из единичной матрицы в результате одного из следующих элементарных преобразований:

Умножение строки (столбца) матрицы на скаляр

Прибавление к какой либо строке (столбцу) матрицы другой строки (столбца), умноженный на скаляр . Элементарные преобразования матрицы — это такие преобразования матрицы, в результате которых сохраняется эквивалентность матриц. Таким образом, элементарные преобразования не изменяют множество решений системы линейных алгебраических уравнений, которую представляет эта матрица.

[16] Курс алгебры / Э. Б. Винберг— 2-е изд., испр. и доп. М.: Изд-во «Факториал Пресс», 2001— С. 164–166.

[17] Основы теории групп / М. И. Каргаполов, Ю. И. Мерзляков. — 3-е изд., перераб. и доп.— М.: Наука, 1982.— С. 27–28.

[18] Введение в теорию групп / П. С. Александров — М.: Издательство «Наука», 1980. — С. 55–56.

[19] Линейная алгебра и некоторые приложения / Л. И. Головина. — 3-е изд., перераб. и доп. — М.: Издательство «Наука», 1979. — С. 276.

[20] Группы и их графы / И. Гроссман, В. Магнус; под ред. В. Е. Тараканова — М.: Издательство «Мир», 1971. — С. 59–60.

 

[21] Тот же.

[22] Теория групп / А. Г. Курош. — М.: Издательство «Наука», 1967. — С. 41.

[23] То есть вершину, соответствующую элементу r.

[24] Произвольный граф называется однородным степени n, если в каждую его вершину входит и из каждой вершины выходит одинаковое число направленных отрезков, равное n. Граф группы будет однородным в этом смысле.

[25] Группы и их графы / И. Гроссман, В. Магнус; под ред. В. Е. Тараканова — М.: Издательство «Мир», 1971. — С. 62–77.