2020-01-14
78
Рассмотрим основные свойства функции распределения, следующие непосредственно из определения:
. (31.1)
1. Введем обозначение: 
. Тогда из определения следует 
. Здесь выражение 
рассматривается как невозможное событие с нулевой вероятностью.
2. Пусть 
. Тогда из определения функции 
следует 
. Случайное событие 
является достоверным и его вероятность равна единице.
3. Вероятность 
случайного события 
, состоящего в том, что случайная величина 
принимает значение из интервала 
при 
определяется через функцию 
следующим равенством
. (31.2)
Для доказательства этого равенства рассмотрим соотношение
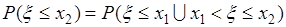. (31.3)
События 
и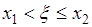 
несовместны, поэтому по формуле сложения вероятностей из (31.3) следует
, (31.4)
что и совпадает с формулой (31.2), поскольку 
и 
.
4. Функция 
является неубывающей. Для доказательства рассмотрим 
. При этом справедливо равенство (31.2). Его левая часть 
, поскольку вероятность принимает значения из интервала 
. Поэтому и правая часть равенства (31.2) неотрицательна: 
, или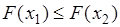 
. Это равенство получено при условии , поэтому - неубывающая функция.
5. Функция непрерывна справа в каждой точке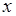 
, т.е.
, (31.5)
где 
- любая последовательность, стремящаяся к 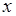справа, т.е. 
и 
.
Для доказательства представим функцию 
в виде: 
. (31.5)
Отсюда
. (31.6)
Теперь на основании аксиомы счетной аддитивности вероятности выражение в фигурных скобках равно 
, таким образом 
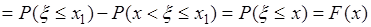, что и доказывает непрерывность справа функции 
.
Таким образом, каждая функция распределения вероятностей обладает свойствами 1-5. Верно и обратное утверждение: если 
, 
, удовлетворяет условиям 1-5,то она может рассматриваться как функция распределения некоторой случайной величины.
