2020-01-14
93
Пусть случайная величина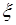 
принимает значения 
с вероятностями 
, 
. Тогда ее функция распределения вероятностей
, (34.1)
где 
- функция единичного скачка. Определить плотность вероятности 
случайной величины 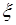по ее функции распределения 
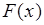можно с учетом равенства 
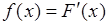. Однако при этом возникают математические сложности, связанные с тем, что функция единичного скачка , входящая в (34.1), имеет разрыв первого рода при 
. Поэтому в точке не существует производная 
функции .
Для преодоления этой сложности вводится 
-функция. Функцию единичного скачка можно представить через -функцию следующим равенством:
. (34.2)
Тогда формально производная
(34.3)
и плотность вероятности дискретной случайной величины определяется из соотношения (34.1) как производная функции 
:
. (34.4)
Функция (34.4) обладает всеми свойствами плотности вероятности. Рассмотрим пример. Пусть дискретная случайная величина 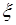принимает значения 
с вероятностями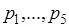 
, и пусть 
, 
. Тогда вероятность 
- того, что случайная величина 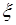примет значение из отрезка 
может быть вычислена, исходя из общих свойств плотности по формуле:
.
Здесь
,
поскольку особая точка 
- функции, определяемая условием 
, находится внутри области интегрирования при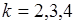 
, а при 
особая точка находится вне области интегрирования. Таким образом,
.
Для функции (34.4) также выполняется условие нормировки:
.
Отметим, что в математике запись вида (34.4) считается некорректной (неправильной), а запись (34.2) - корректной. Это обусловлено тем, что 
-функция при нулевом аргументе 
, и говорят, что 
не существует. С другой стороны, в (34.2) -функция содержится под интегралом. При этом правая часть (34.2) - конечная величина для любого 
, т.е. интеграл от -функции существует. Несмотря на это в физике, технике и других приложениях теории вероятностей часто используется представление плотности в виде (34.4), которое, во-первых, позволяет получать верные результаты, применяя свойства - функции, и во-вторых, имеет очевидную физическую интерпретацию.
