2020-01-14
79
Пусть случайная величина 
имеет дифференцируемую функцию распределению вероятностей 
, тогда функция
(33.1)
называется плотностью распределения вероятностей (или плотностью вероятности) случайной величины , а случайная величина - непрерывной случайной величиной.
Рассмотрим основные свойства плотности вероятности.
Из определения производной следует равенство:
. (33.2)
Согласно свойствам функции имеет место равенство 
. Поэтому (33.2) принимает вид:
. (33.3)
Это соотношение объясняет название функции 
. Действительно, согласно (33.3) функция 
- это вероятность 
, приходящаяся на единицу интервала 
, в точке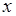 
, поскольку 
. Таким образом, плотность вероятности, определяемая соотношением (33.3), аналогична определениям плотностей других величин, известных в физике, таких как плотность тока, плотность вещества, плотность заряда и т.д.
2. Поскольку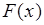 
- неубывающая функция, то ее производная 
- функция неотрицательная:
|
|
|
. (33.4)
3. Из (33.1) следует
,
поскольку 
. Таким образом, справедливо равенство
. (33.5)
4. Поскольку 
, то из соотношения (33.5) следует
(33.6)
- равенство, которое называется условием нормировки. Его левая часть 
- это вероятность достоверного события.
5. Пусть 
, тогда из (33.1) следует
. (33.7)
Это соотношение имеет важное значение для приложений, поскольку позволяет вычислить вероятность 
через плотность вероятности 
или через функцию распределения вероятностей 
. Если положить 
, то из (33.7) следует соотношение (33.6).
На рис. 33.1 представлены примеры графиков функции распределения и плотности вероятностей.
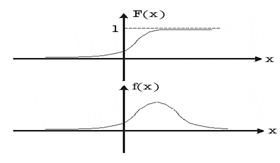
Рис. 33.1. Примеры функции распределения вероятностей и плотности вероятности.
Отметим, что плотность распределения вероятности может иметь несколько максимумов. Значение 
аргумента 
, при котором плотность имеет максимум называется модой распределения случайной величины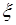 
. Если плотность имеет более одной моды, то 
называется многомодальной.
