Характеристическая функция

Характеристической функцией случайной величины  называется функция

    , .                         (46.1)

Пусть  - непрерывная случайная величина с плотностью вероятности 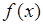, тогда ее характеристическая функция

                                (46.2)

- является интегральным преобразованием, которое называется преобразованием Фурье от плотности вероятности 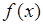. Известно, что преобразование Фурье является взаимно однозначным. Поэтому существует обратное преобразование, которое определяет плотность вероятности  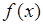через характеристическую функцию . Это преобразование имеет вид

    .                            (46.3)

Соотношения (46.2) и (46.3) образуют пару преобразований Фурье.

Для дискретной случайной величины , принимающей значения 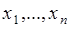 с вероятностями  характеристическая функция, как следует из (46.1), имеет вид

    .                                         (46.4)

Характеристическая функция является полной вероятностной характеристикой случайной величины, также как и функция распределения  или плотность вероятности 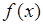. Смысл введения характеристической функции в теории вероятности состоит в том, что имеется класс задач, которые относительно просто решаются с применением преобразования Фурье от плотности вероятности. Роль этого преобразования оказалась столь велика, что в теории появился специальный термин «характеристическая функция» для обозначения этого преобразования.