Основные свойства характеристической функции

 

Рассмотрим свойства функции  для непрерывной случайной величины. Для дискретной величины эти свойства доказываются аналогично.

1). В общем случае характеристическая функция (46.2) является комплексной. Ее вещественная часть

                                (47.1)

- является - преобразованием от плотности вероятности, и мнимая часть

                                 (47.2)

- является - преобразованием от . Если 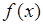 - четная функция, то , тогда характеристическая функция 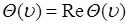 и является вещественной и четной функцией.

2). . Это свойство следует из (46.2) и условия нормировки для плотности:

    .                            (47.3)

3).  - функция  имеет глобальный максимум в точке . Доказательство следует из (46.2):

.

4).

5). Характеристическая функция непрерывна. Для доказательства рассмотрим приращение  аргумента функции , такое, что 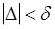, где  - положительное число. Тогда имеет место следующая цепочка преобразований:

   

    .                        (47.4)

Пусть  и число

,      (47.5)

тогда из (47.4) следует

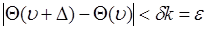.                  (47.6)

Таким образом, выполняется определение непрерывности функции : для любого  можно выбрать положительное , что из условия  следует .

 

Примеры вычисления характеристической функции

48.1. Пусть  - случайная величина с характеристической функцией . Найти характеристическую функцию  случайной величины

    ,                                          (48.1)

где - числа. По определению

    .            (48.2)

48.2. Найти характеристическую функцию  гауссовой случайной величины . По формуле (46.2)

    .       (48.3)

Выполним замену переменной интегрирования  на переменную , тогда   и

    .            (48.4)

Показатель в подынтегральном выражении преобразуем следующим образом:

.

Подстановка этого результата в (48.4) приводит к выражению

    .                                  (48.5)

Отсюда следует, что характеристическая функция гауссовой случайной величины  при  является вещественной и четной функцией.