Пусть 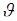 - неизвестный параметр (число), характеризующий состояние системы. Для определения параметра
- неизвестный параметр (число), характеризующий состояние системы. Для определения параметра 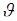 проводится опыт (измерение). Ситуация осложняется тем, что в процессе измерения на величину
проводится опыт (измерение). Ситуация осложняется тем, что в процессе измерения на величину 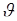 накладывается помеха. Таким образом, измерению подлежит не число
накладывается помеха. Таким образом, измерению подлежит не число 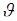 , а некоторая случайная величина
, а некоторая случайная величина 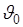 , значения которой в каждом опыте точно предсказать невозможно.
, значения которой в каждом опыте точно предсказать невозможно.
Случайную величину 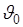 будем называть оценкой параметра
будем называть оценкой параметра 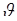 . Тогда
. Тогда 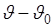 - ошибка, также случайная величина. Характеристикой качества оценки
- ошибка, также случайная величина. Характеристикой качества оценки 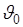 является ее среднеквадратическая ошибка
является ее среднеквадратическая ошибка
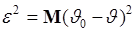 . (45.1)
. (45.1)
Преобразуем это выражение:
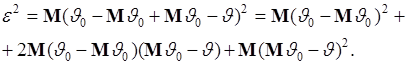 (45.2)
(45.2)
Величина 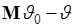 - детерминированная, поэтому ее можно вынести за оператор
- детерминированная, поэтому ее можно вынести за оператор 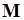 , следовательно, второе слагаемое
, следовательно, второе слагаемое
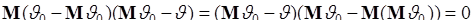
Первое слагаемое (45.2) по определению
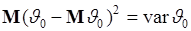
- дисперсия случайной величины 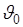 . Введем обозначение
. Введем обозначение
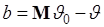 . (45.3)
. (45.3)
Число 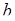 называется смещением оценки
называется смещением оценки 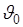 . Таким образом, из (45.2) следует
. Таким образом, из (45.2) следует
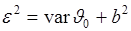 (45.4)
(45.4)
- среднеквадратическая ошибка является суммой двух неотрицательных слагаемых. Первое из них – дисперсия, или случайная (стохастическая) компонента ошибки, а второе – квадрат смещения – систематическая ошибка. Если 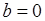 , то оценка
, то оценка 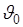 называется несмещенной.
называется несмещенной.
Пусть случайная величина 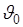 - имеет плотность вероятности
- имеет плотность вероятности 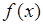 . Тогда процедуре измерения можно дать геометрическую интерпретацию. На рис. 45.1 представлен график плотности вероятности оценки и показана систематическая ошибка
. Тогда процедуре измерения можно дать геометрическую интерпретацию. На рис. 45.1 представлен график плотности вероятности оценки и показана систематическая ошибка 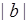 , и случайная ошибка
, и случайная ошибка 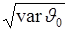 .
.
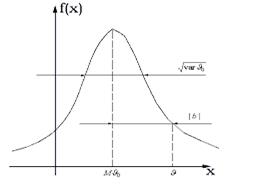
Рис. 45.1. Плотность вероятности оценки,
случайная и систематическая части ошибки.
Очевидно, идеальная процедура измерения (с нулевой среднеквадратической ошибкой) – это процедура, для которой плотность 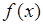 близка к функции
близка к функции 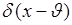 . Тогда
. Тогда 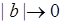 , точка
, точка 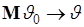 , а эффективная ширина
, а эффективная ширина 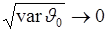 .
.
 2020-01-14
2020-01-14 154
154








