Анализ ряда распределения

Для оценки расхождения теоретического и фактического распределений используется показатель асимметрии - К_а, который рассчитывается по формуле:

                                                                                          (1.26)

где  - коэффициент ассиметрии;

 - средняя арифметическая взвешенная;

 - мода;

 - среднее квадратическое отклонение для сгруппированного признака.

 

Для распределения групп по объему производства:

Так как Ка>0, то распределение правостороннее. Асимметрия несущественна, так как . Где

Для распределения групп по уровню фондоотдачи:

Так как Ка>0, то распределение правостороннее. Асимметрия несущественна, так как 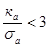. Где

Для симметричных распределений так же рассчитывается показатель эксцесса. Наиболее точным является показатель, основанный на использовании центрального момента четвертого порядка:

                                             (1.27)

где - момент четвертого порядка;

 - эксцесс;

 - среднее квадратическое отклонение для сгруппированного признака.

Центральный момент четвертого порядка рассчитывается по формуле:

                                        (1.28)

где  - центральный момент четвертого порядка;

 - центральный вариант соответствующего интервала;

 - средняя арифметическая взвешенная;

 - частота соответствующей группы.

Для распределения групп по уровню объема производства:

Так как эксцесс<0, то распределение групп по уровню объема производства низковершинное.

Для распределения групп по уровню фондоотдачи:

Так как эксцесс<0, то распределение групп по фондоотдаче низковершинное.

Распределение можно считать нормальным, если показатели асимметрии и эксцесса не превышают своих двукратных средних квадратических отклонений:

,                                (1.29)

                                        ,                         (1.30)

где n – число единиц совокупности.

 

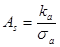                                        ,                                                            (1.31)

Для групп по объему производства:

несущественна.

Для групп по уровню фондоотдачи:

 несущественна.

                                      ,                                                            (1.32)

Для групп по объему производства:

Для групп по уровню фондоотдачи:

Для оценки степени согласия теоретического и фактического распределений воспользуемся критериями согласия Пирсона (), Колмогорова (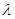) и Романовского (K).

Критерий Пирсона вычисляется по формуле:

                                   (1.33)

где 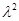 - критерий согласия Пирсона;

 - эмпирические частоты;

 - теоретические частоты.

Таблица 1.8 - Расчет эмпирических и теоретических частот по уровню объема производства

Группы по уровню объема производства	Код строки	Частоты ряда распределения		Накопленные частоты		‌‌‌׀fэ-fт׀
		fэ	fт	fэ	fт
А	Б	1	2	3	4	5
296-301	1	3	2	3	2	1
301-306	2	6	4	9	6	3
306-311	3	7	6	16	12	4
311-316	4	3	6	19	18	1
316-321	5	3	4	22	22	0
321-326	6	3	3	25	25	0
326-331	7	2	2	27	27	0
Итого	8	27	27

 

Таблица 1.9 - Расчет эмпирических и теоретических частот по уровню фондоотдачи

Группы по уровню фондоотдачи	Код строки	Частоты ряда распределения		Накопленные частоты		|fэ-fт|
		fэ	fт	fэ	fт
А	Б	1	2	3	4	5
0,91-0,96	1	5	4	5	4	1
0,96-1,01	2	6	6	11	10	1
1,01-1,06	3	7	7	18	17	1
1,06-1,11	4	5	6	23	23	0
1,11-1,16	5	4	4	27	27	0
Итого	6	27	27

Критерий Пирсона:

Для распределения групп по уровню объема производства:

Исходя из данных таблицы вероятность соответствия фактического распределения теоретическому - 99%(К=2).

Для распределения групп по уровню фондоотдачи:

 

Исходя из данных таблицы вероятность соответствия фактического распределения теоретическому 90%(К=1).

 

Критерий Колмогорова:

                                                 (1.34)

где D - максимальная разница между накопленными теоретическими и фактическими частотами.

Для распределения групп  по уровню объема производства:

D = 3

p=0,86

Вероятность соответствия фактического распределения теоретическому - 86%.

Для распределения групп по уровню фондоотдачи:

D = 1,

p=1

Вероятность соответствия фактического распределения теоретическому - 100%.

Критерий Романовского вычисляется по формуле:

,                                    (1.35)

где  - критерий Романовского;

 - критерий Пирсона;

k – количество групп.

Для распределения групп  по уровню объема производства:

<3, следовательно, различия между эмпирическим и теоретическим распределениями несущественны.

Для распределения групп по уровню фондоотдачи:

<3, следовательно, различия между эмпирическим и теоретическим распределениями несущественны.