2020-01-14
97
Для построения поля корреляции факторный признак (объем производства) расположим на оси абсцисс (X), а зависимый (фондоотдача) на оси ординат (Y).
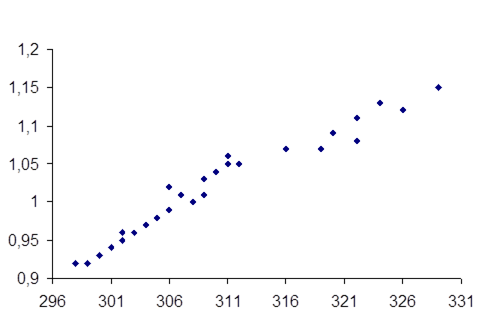
Условные обозначения:
х – объем производства;
у – фондоотдача.
Рисунок 1.13- поле корреляции
Так как параметр а1 зависит от единиц измерения факторов х и у, то для оценки связи без влияния единиц измерения используется показатель - коэффициент эластичности, который рассчитывается по формуле:
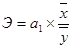, (1.36)
где Э – коэффициент эластичности;
a1 – коэффициент при х в уравнении прямой;
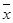- среднее значение факторного признака;
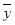- среднее значение зависимого признака.
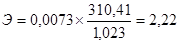
При росте фондовооруженности на 1% объем производства возрастает на 2,22%. Коэффициентом, показывающим не только тесноту связи, но и ее направление является линейный коэффициент корреляции (r), который определяется по формуле:
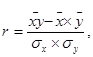(1.37)
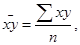(1.38)
где r – линейный коэффициент корреляции;
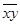- среднее произведение факторного признака на зависимый;
xy – произведение факторного признака на зависимый;
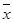- простая средняя арифметическая факторного признака;
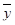- простая средняя арифметическая зависимого признака;
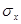- среднее квадратическое отклонение по зависимому признаку;
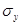- среднее квадратическое отклонение по факторному признаку.
Используя данные табл. 1.11, получаем:
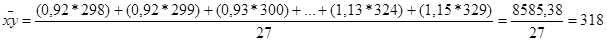
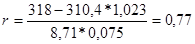
Связь между признаками прямая (так как r>0), тесная (так как r близок к 1).
Рассчитаем эмпирическое корреляционное отношение по формуле:
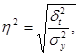(1.39)
где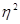 
- эмпирическое корреляционное отношение;
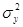- общая дисперсия зависимого признака;
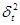- межгрупповая дисперсия зависимого признака.
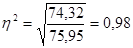
Для оценки тесноты связи используется показатель - теоретическое корреляционное отношение, который определяется по формуле:
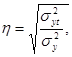(1.40)
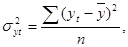(1.41)
где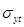 
- остаточная дисперсия;
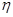- теоретическое корреляционное отношение;
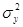- общая дисперсия зависимого признака по несгруппированным данным;
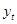- теоретическое значение;
- простая средняя арифметическая эмпирического ряда;
n – численность совокупности.
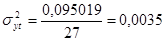
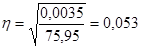
Так как 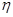неблизок к 1, то связь между признаками не тесная.
Рассчитаем коэффициенты корреляции рангов Кенделла и Спирмена, а также коэффициент Фехнера.
Коэффициент Спирмена вычисляется по формуле:
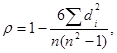(1.42)
где d - разности между рангами в двух рядах;
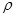- коэффициент корреляции рангов Спирмена;
n – численность совокупности.
Коэффициент Кенделла - по формуле:
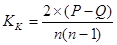, (1.43)
где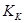 
- коэффициент Кенделла;
P – сумма значений рангов, расположенных ниже соответствующего порядкового номера ранга и больше его;
Q – сумма значений рангов, расположенных ниже соответствующего порядкового номера ранга и меньше его;
n – численность совокупности.
Коэффициент Фехнера – по формуле:
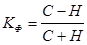, (1.44)
где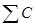 
– число совпадений знаков отклонений признаков от средней;
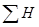- число совпадений знаков;
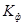- коэффициент Фехнера.
Таблица 1.13
Данные для расчета коэффициентов Кендалла, Спирмена и Фехнера
| Х | Код строки | +, - | Y | +, - | Ранг Х | Ранг Y | (уt -y) 2 | P | Q |
| А | Б | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 298 | 1 | - | 0,92 | - | 1 | 1,5 | 0,0069 | 25 | 0 |
| 299 | 2 | - | 0,92 | - | 2 | 1,5 | 0,0069 | 25 | 0 |
| 300 | 3 | - | 0,93 | - | 3 | 3 | 0,0053 | 24 | 0 |
| 301 | 4 | - | 0,94 | - | 4 | 4 | 0,0040 | 23 | 0 |
| 302 | 5 | - | 0,95 | - | 5,5 | 5 | 0,0040 | 22 | 0 |
| 302 | 6 | - | 0,96 | - | 5,5 | 6,5 | 0,0040 | 20 | 0 |
| 303 | 7 | - | 0,96 | - | 7 | 6,5 | 0,0028 | 20 | 0 |
| 304 | 8 | - | 0,97 | - | 8 | 8 | 0,0018 | 19 | 0 |
| 305 | 9 | - | 0,98 | - | 9 | 9 | 0,0011 | 18 | 0 |
| 306 | 10 | - | 0,99 | - | 10,5 | 10 | 0,0011 | 17 | 0 |
| 308 | 11 | - | 1,00 | - | 13 | 13 | 0,0002 | 13 | 1 |
| 309 | 12 | - | 1,01 | - | 14,5 | 13 | 0,000009 | 13 | 1 |
| 307 | 13 | - | 1,01 | - | 12 | 13 | 0,00053 | 13 | 1 |
| 306 | 14 | - | 1,02 | - | 10,5 | 11 | 0,0011 | 13 | 0 |
| 309 | 15 | - | 1,03 | + | 14,5 | 15 | 0,000009 | 12 | 0 |
| 310 | 16 | - | 1,04 | + | 16 | 16 | 0,000009 | 11 | 0 |
| 311 | 17 | + | 1,06 | + | 17,5 | 17 | 0,000036 | 10 | 0 |
| 312 | 18 | + | 1,05 | + | 19 | 18,5 | 0,00029 | 8 | 0 |
| 311 | 19 | + | 1,05 | + | 17,5 | 18,5 | 0,000036 | 8 | 0 |
| 316 | 20 | + | 1,07 | + | 20 | 20,5 | 0,0022 | 6 | 0 |
| 319 | 21 | + | 1,07 | + | 21 | 20,5 | 0,0045 | 6 | 0 |
| 322 | 22 | + | 1,08 | + | 23,5 | 23 | 0,0076 | 4 | 1 |
| 320 | 23 | + | 1,09 | + | 22 | 22 | 0,0059 | 4 | 0 |
| 322 | 24 | + | 1,11 | + | 23,5 | 24 | 0,0076 | 3 | 0 |
| 326 | 25 | + | 1,12 | + | 26 | 26 | 0,0137 | 1 | 1 |
| 324 | 26 | + | 1,13 | + | 25 | 25 | 0,0115 | 1 | 0 |
| 329 | 27 | + | 1,15 | + | 27 | 27 | 0,0019 | 0 | 0 |
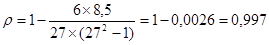
Значит, связь между признаками прямая, тесная.
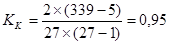
В 95 случаях из 100 при изменении ранга х изменяется ранг у.
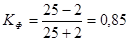
Значит, связь между признаками прямая, тесная.
Так как объем изучаемой совокупности невелик, то могут возникнуть сомнения в том, что обнаруженная связь носит закономерный характер, несмотря на её теоретическую обоснованность. Для более полной оценки связи необходимо проверить её значимость.
Рассчитаем критерий Фишера, который равен:
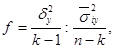(1.45)
где f – коэффициент Фишера;
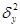- межгрупповая дисперсия;
k – количество групп;
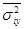- средняя из внутригрупповых дисперсия;
n – численность совокупности.
По уровню объема производства:
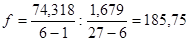
По уровню фондоотдачи:
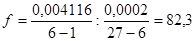
Табличное значение при k1=20, k2=5 равно: Fтабл. = 4,56 (при р=0,01)
Так как Fрасч>Fтабл, то значимость найденной зависимости подтверждается с вероятностью 95%..
2. Ряды динамики
Рядом динамики называется ряд статистических показателей, характеризующих изменение общественных явлений во времени.
В результате статистического наблюдения получены данные, характеризующие урожайность зерновых культур по Свердловской области. Эти данные представлены в таблице 2.1.
Таблица 2.1 - Урожайность зерновых культур
| Годы | Урожайность зерновых культур |
| 1995 | 16,0 |
| 2001 | 16,3 |
| 2002 | 16,6 |
| 2003 | 15,4 |
| 2004 200 | 12,4 |
| 2005 | 7,0 |
Поиск недостающих данных ряда динамики осуществляется по формулам:
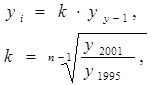(2.1)
где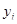 
- уровень динамического ряда в соответствующем году;
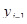- уровень динамического ряда в (соответствующем году минус 1);
k – средний коэффициент роста;
n – число уровней ряда в данном периоде;
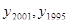- уровни динамического ряда в 2001 и 1995 годах.
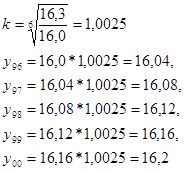
Таблица 2.2 - Урожайность зерновых культур
| Годы | Урожайность зерновых культур |
| 1995 | 16,0 |
| 1996 | 16,04 |
| 1997 | 16,08 |
| 1998 | 16,12 |
| 1999 | 16,16 |
| 2000 | 16,2 |
| 2001 | 16,3 |
| 2002 | 16,6 |
| 2003 | 15,4 |
| 2004 | 12,4 |
| 2005 | 7,0 |
