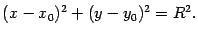Определение. В декартовой прямоугольной системе координат вектор с компонентами (А, В) перпендикулярен прямой, заданной уравнением Ах + Ву + С = 0. Пример. Найти уравнение прямой, проходящей через точку А(1, 2) перпендикулярно вектору  (3, -1). Составим при А = 3 и В = -1 уравнение прямой: 3х – у + С = 0. Для нахождения коэффициента С подставим в полученное выражение координаты заданной точки А. Получаем: 3 – 2 + C = 0, следовательно С = -1. Итого: искомое уравнение: 3х – у – 1 = 0. Уравнение прямой, проходящей через две точки. Пусть в пространстве заданы две точки M1(x1, y1, z1) и M2(x2, y2, z2), тогда уравнение прямой, проходящей через эти точки:
(3, -1). Составим при А = 3 и В = -1 уравнение прямой: 3х – у + С = 0. Для нахождения коэффициента С подставим в полученное выражение координаты заданной точки А. Получаем: 3 – 2 + C = 0, следовательно С = -1. Итого: искомое уравнение: 3х – у – 1 = 0. Уравнение прямой, проходящей через две точки. Пусть в пространстве заданы две точки M1(x1, y1, z1) и M2(x2, y2, z2), тогда уравнение прямой, проходящей через эти точки:  Если какой- либо из знаменателей равен нулю, следует приравнять нулю соответствующий числитель. На плоскости записанное выше уравнение прямой упрощается:
Если какой- либо из знаменателей равен нулю, следует приравнять нулю соответствующий числитель. На плоскости записанное выше уравнение прямой упрощается:  если х1 ¹ х2 и х = х1, еслих1 = х2. Дробь
если х1 ¹ х2 и х = х1, еслих1 = х2. Дробь  = k называется угловым коэффициентом прямой.
= k называется угловым коэффициентом прямой.
Пример. Найти уравнение прямой, проходящей через точки А(1, 2) и В(3, 4). Применяя записанную выше формулу, получаем: 
Уравнение прямой по точке и угловому коэффициенту. Если общее уравнение прямой Ах + Ву + С = 0 привести к виду:  и обозначить
и обозначить  , то полученное уравнение называется уравнением прямой с угловым коэффициентом k.
, то полученное уравнение называется уравнением прямой с угловым коэффициентом k.
Вопрос 2: Определение производной. Геометрический и экономический смысл:
Определение: Рассмотрим y=f(x): производной функцией в фиксированной точке называется lim отношения приращения этой функцией в данной точке к бесконечно малому приращению аргумента.
 (y’;
(y’;  ;
;  )
)
Рассмотрим приращение функции y=f(x). Зафиксируем x=x0

Геометрический смысл производной состоит в том, что производная вычисляет в абсциссе точку касания, численно равную k.
y’=  =k
=k
Экономический смысл производной: производная в экономическом смысле характеризует приближенно дополнительные затраты на производство единицы дополнительной продукции.

Билет 10:
Вопрос 1: Условие параллельности и перпендикулярности прямых на плоскости:
Из общего уравнения прямой на плоскости Оху Ax+By+C=0 получаем частные случаи, из двух таких случаев:
1). A  0, B=0. Ax+C=0, или x=a, a=
0, B=0. Ax+C=0, или x=a, a=  : эта прямая параллельна оси Оу и отсекает на оси Ох отрезок, имеющий величину а. При С=0 прямая совпадает с осью Оу
: эта прямая параллельна оси Оу и отсекает на оси Ох отрезок, имеющий величину а. При С=0 прямая совпадает с осью Оу
2). А=0, В  0. Ву+С=О, параллельна оси Ох, или у=b, b=
0. Ву+С=О, параллельна оси Ох, или у=b, b=  , где b – величина отрезка, отсекаемого прямой на оси Оу.
, где b – величина отрезка, отсекаемого прямой на оси Оу.
Следуют признаки параллельности и перпендикулярности прямых:
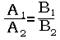
A1A2+B1B2=0
Если прямые заданны в форме у=kx+b с угловыми коэффициентами k1 и k2 , то угол между ними вычисляется по формуле:

В этом случае условие параллельности прямых на плоскости будет k1=k2, а перпендикулярности k1= 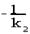 .
.
Вопрос 2: Уравнение касательной и нормали:
Уравнение касательной:

Уравнение нормали:
Уравнение нормали к поверхности F(x;y;z)=0 в точке M0(x0;y0;z0) имеет вид:

Билет 11:
Вопрос 1: Каноническое уравнение прямой в пространстве:

Замечание 1: Эта компактная запись на самом деле содержит три уравнения.
Замечание 2: Это формальная запись и выражение вида  в данном случае допустимо.
в данном случае допустимо.
Замечание 3: Надо понимать, что для уравнения плоскости (прямой) играет роль именно направление перпендикулярного (направляющего) вектора, а не он сам. Т.о. вполне допустимо из каких-либо соображений заменять данный (или полученный в ходе решения) вектор на пропорциональный ему. Целесообразно также упрощать полученное уравнение, деля все его коэффициенты на общий множитель.
Вопрос 2: Правило дифференцирования:
Если функции f и g дифференцируемы в точке  то в этой же точке дифференцируемы сумма, произведение и частное (если
то в этой же точке дифференцируемы сумма, произведение и частное (если  ) этих функций, причем
) этих функций, причем
|
Доказательство:
а) 
По свойству предела суммы получаем 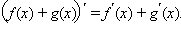
Постоянный множитель C можно выносить из-под знака производной:

|
В частности,

|
б) Функцию f · g можно записать в виде  Но
Но 
По свойству предела произведения получаем 
Используя доказанное равенство, получим, что 
Раскрывая скобки и приводя подобные члены, получим формулу 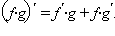
в) Для доказательства этой формулы заметим, что 
Воспользовавшись свойством предела частного, получим 
После этого представим  как произведение функций f и
как произведение функций f и  откуда и следует доказываемая формула.
откуда и следует доказываемая формула.
Если f дифференцируема, то 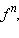 где
где  также дифференцируема, причем
также дифференцируема, причем

|
Доказательство этой формулы предоставляем читателю.
Если функция y = f (x) непрерывна и строго возрастает в окрестности точки  причем
причем  то функция x = φ (y), обратная к функции y = f (x), дифференцируема в точке y0 = f (x0), причем
то функция x = φ (y), обратная к функции y = f (x), дифференцируема в точке y0 = f (x0), причем

|
Если функции y = f (x) и z = g (y) дифференцируемы в точках x0 и y0 = f (x0) соответственно, то сложная функция z = g (f (x)) дифференцируема в точке x0, причем
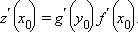
|
Следствием этой теоремы является тот факт, что дифференциал функции y = f (x) имеет один и тот же вид 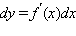 как в случае, когда x – независимая переменная, так и в случае, когда x – дифференцируемая функция другого переменного.
как в случае, когда x – независимая переменная, так и в случае, когда x – дифференцируемая функция другого переменного.
Если f (x) – четная функция, то  – нечетная; если f (x) – нечетная функция, то
– нечетная; если f (x) – нечетная функция, то  – четная.
– четная.
Пусть в окрестности точки t0 определены функции x (t) и y (t), причем x (t) непрерывна и строго монотонна. Пусть в этой окрестности существуют производные 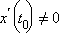 и
и  Тогда сложная функция y = y (t (x)), где t (x) – функция, обратная x (t), дифференцируема по x, причем
Тогда сложная функция y = y (t (x)), где t (x) – функция, обратная x (t), дифференцируема по x, причем

|
Билет 12:
Вопрос 1: Условия параллельности и перпендикулярности прямых в пространстве:
Чтобы две прямые были параллельны необходимо и достаточно, чтобы направляющие векторы этих прямых были коллинеарны, т.е. их соответствующие координаты были пропорциональны.

Чтобы две прямые были перпендикулярны необходимо и достаточно, чтобы направляющие векторы этих прямых были перпендикулярны, т.е. косинус угла между ними равен нулю.

Вопрос 2: Производная от сложной функции. Доказательство:
Теорема. Пусть сложная функция y=f(  (x)) такова, что функция y=f(х0) определена на промежутке T, а функция t=
(x)) такова, что функция y=f(х0) определена на промежутке T, а функция t=  (x) определена на промежутке X и множество всех ее значений входит в промежуток T. Пусть функция t=
(x) определена на промежутке X и множество всех ее значений входит в промежуток T. Пусть функция t=  (x) имеет производную в каждой точке внутри промежутка X, а функция y=f(t) имеет производную в каждой точке промежутка T. Тогда функция y=f(
(x) имеет производную в каждой точке внутри промежутка X, а функция y=f(t) имеет производную в каждой точке промежутка T. Тогда функция y=f(  (x)) имеет производную в каждой точке внутри промежутка, вычисляемую по формуле
(x)) имеет производную в каждой точке внутри промежутка, вычисляемую по формуле  .
.
Доказательство:
Так как функция y=f(x) дифференцируема в точке х0, то приращение этой функции в точке х0 может быть записано в виде:

Где  .
.
Поделив равенство (1) на  , получим:
, получим:

Равенство (2) справедливо для любых достаточно малых х.
Возьмём 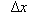 равное приращению функции x=
равное приращению функции x=  , соответствующего приращению
, соответствующего приращению  аргумента t в точке t0, и устремим в этом равенстве
аргумента t в точке t0, и устремим в этом равенстве 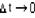 .
.
Так как по условию функция x=  имеет в точке t0 производную, то она непрерывна в этой точке. Следовательно, согласно определению непрерывной функции в точке,
имеет в точке t0 производную, то она непрерывна в этой точке. Следовательно, согласно определению непрерывной функции в точке,  при
при  . Но тогда и
. Но тогда и  также стремится к 0, то есть имеем
также стремится к 0, то есть имеем

В силу соотношения (3) существует предел правой части равенства (2) при  , равный
, равный  . Значит существует предел при
. Значит существует предел при  и левые части равенства (2), который по определению производной равно производной сложной функции y=f[
и левые части равенства (2), который по определению производной равно производной сложной функции y=f[ 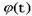 ] в точке t0, тем самым доказывается дифференцируемость сложной функции и устанавливается формула
] в точке t0, тем самым доказывается дифференцируемость сложной функции и устанавливается формула  .
.
Билет 13:
Вопрос 1: Условия параллельности и перпендикулярности прямой и плоскости:
Для того, чтобы прямая и плоскость были параллельны, необходимо и достаточно, чтобы вектор нормали к плоскости и направляющий вектор прямой были перпендикулярны. Для этого необходимо, чтобы их скалярное произведение было равно нулю.
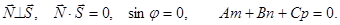
Для того, чтобы прямая и плоскость были перпендикулярны, необходимо и достаточно, чтобы вектор нормали к плоскости и направляющий вектор прямой были коллинеарные. Это условие выполняется, если векторное произведение этих векторов было равно нулю.

Вопрос 2: Производная от неявной и параметрически заданной функции:
Производная функции, заданной неявно:
Уравнение вида  , содержащее переменные
, содержащее переменные 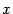 и
и 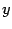 , иногда можно разрешить относительно
, иногда можно разрешить относительно 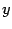 и получить в явном виде зависимость
и получить в явном виде зависимость  . Например, если дано уравнение
. Например, если дано уравнение  , то из него можно получить зависимость
, то из него можно получить зависимость  . Однако такое явное выражение
. Однако такое явное выражение 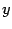 через
через 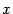 , использующее лишь элементарные функции, можно получить не из любого уравнения вида
, использующее лишь элементарные функции, можно получить не из любого уравнения вида  (даже если в самом уравнении участвуют лишь элементарные функции).
(даже если в самом уравнении участвуют лишь элементарные функции).
Покажем, как, используя уравнение  , найти производную
, найти производную  , не выражая
, не выражая 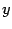 через
через 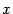 в явном виде. Для этого найдём производные левой и правой части уравнения по переменной
в явном виде. Для этого найдём производные левой и правой части уравнения по переменной 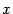 , считая
, считая  промежуточным аргументом, а потом выразим
промежуточным аргументом, а потом выразим  из получающегося равенства.
из получающегося равенства.
Производные функции, заданной параметрически:
Пусть задана зависимость двух переменных 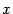 и
и 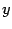 от параметра
от параметра  , изменяющегося в пределах от
, изменяющегося в пределах от 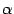 до
до 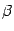 :
:

Пусть функция 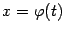 имеет обратную:
имеет обратную:  . Тогда мы можем, взяв композицию функций
. Тогда мы можем, взяв композицию функций  и
и  , получить зависимость
, получить зависимость 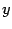 от
от 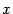 :
: 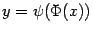 . Зависимость величины
. Зависимость величины 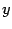 от величины
от величины 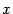 , заданная через зависимость каждой из них от параметра
, заданная через зависимость каждой из них от параметра  в виде
в виде  , называется функцией
, называется функцией  , заданной параметрически.
, заданной параметрически.
Производную функции  , заданной параметрически, можно выразить через производные функций
, заданной параметрически, можно выразить через производные функций  и
и  : поскольку
: поскольку 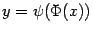 и, по формуле производной обратной функции,
и, по формуле производной обратной функции,  , то
, то

где  - значение параметра, при котором получается интересующее нас при вычислении производной значение
- значение параметра, при котором получается интересующее нас при вычислении производной значение 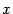 .
.
Заметим, что применение формулы приводит нас к зависимости между  и
и 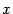 , снова выраженной в виде параметрической зависимости:
, снова выраженной в виде параметрической зависимости:  ,
,  ; второе из этих соотношений - то же, что участвовало в параметрическом задании функции
; второе из этих соотношений - то же, что участвовало в параметрическом задании функции  . Несмотря на то, что производная не выражена через
. Несмотря на то, что производная не выражена через 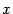 в явном виде, это не мешает решать нам задачи, связанные с нахождением производной, найдя соответствующее значение параметра
в явном виде, это не мешает решать нам задачи, связанные с нахождением производной, найдя соответствующее значение параметра  .
.
Билет 14:
Вопрос 1: Определение окружности. Вывод уравнения:
Определение: Окружностью называется геометрическое место точек плоскости, равноудаленных от фиксированной точки, называемой центром окружности.
Получим уравнение окружности, если известны ее центр и радиус.
Теорема: Окружность радиуса  с центром в точке
с центром в точке  имеет уравнение
имеет уравнение
|
| (1) |
Доказательство. Пусть 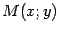 -- текущая точка окружности. По определению окружности расстояние
-- текущая точка окружности. По определению окружности расстояние  равно
равно  (рис. 12.1)
(рис. 12.1)

Рис.12.1.Окружность
По формуле для плоскости получаем, что точки окружности и только они удовлетворяют уравнению

Обе части уравнения неотрицательны. Поэтому после возведения их в квадрат получим эквивалентное уравнение (1).
Если в уравнении (1) раскрыть скобки и привести подобные члены, то вид его изменится. Однако любое уравнение окружности с помощью тождественных преобразований можно привести к виду (1). Для этого достаточно выделить полные квадраты по переменным  и
и  .
.
Вопрос 2: Логарифмическое дифференцирование:
Если требуется найти  из уравнения
из уравнения 
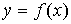 , то можно:
, то можно:
 2020-01-14
2020-01-14 454
454