А) логарифмировать обе части уравнения

;

б ) дифференцировать обе части полученного равенства, где есть сложная функция от х,

.

в) заменить его выражением через х

.

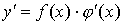Билет 15:

Вопрос 1: Определение эллипса. Вывод уравнения:

Определение: Эллипсом называется геометрическое место точек плоскости, для каждой из которых сумма расстояний до двух данных точек той же плоскости, назывемых фокусами эллипса, есть величина постоянная.

эллипс - это кривая, получающаяся как проекция на плоскость окружности, лежащей в плоскости, которая образует острый угол с плоскостью .

В отличие от окружности, записать в "удобном" виде уравнение эллипса в произвольной системе координат не удается. Поэтому для фиксированного эллипса приходится подбирать систему координат так, чтобы его уравнение было достаточно простым.

Пусть и 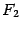- фокусы эллипса. Начало системы координат расположим на середине отрезка . Ось направим вдоль этого отрезка, ось - перпендикулярно к этому отрезку (рис. 1).

Теорема 1: Пусть сумма расстояний от точки эллипса до фокусов равна 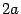, а расстояние между фокусами - . Тогда в выбранной системе координат эллипс имеет уравнение

(1)

где

(2)

Доказательство. Пусть 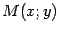-- текущая точка эллипса. По определению эллипса . Из треугольника (рис. 12.3) видно, что , то есть , , и поэтому число существует.

Рис.1.

Фокусами в выбранной системе координат являются точки , . По формуле для плоского случая находим

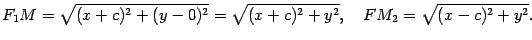
Тогда по определению эллипса

Перенесем один из корней вправо и обе части возведем в квадрат:

После того, как раскроем скобки и приведем подобные члены, приходим к выражению

Разделим обе части этого уравнения на 4 и возведем в квадрат

Раскроем скобку и приведем подобные члены

Учитывая, что , имеем равенство

Наконец, разделив обе части на , получим уравнение (3).

Уравнение (3) называется каноническим уравнением эллипса.

Рис.2. Эллипс

Вопрос 2: Теорема Ферма:

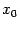Теорема: Пусть функция имеет на множестве точку экстремума , причём множество содержит некоторую -окрестность точки . Тогда либо имеет в точке 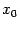производную, равную 0, то есть 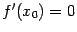, либо производная в точке 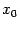не существует.

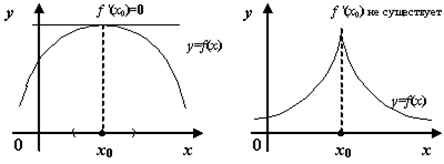
Рис.5.1.Поведение функции в окрестности точки экстремума

Геометрический смысл: Заметим, что условие 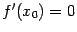означает, что тангенс угла 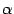наклона касательной к графику 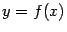, проведённой при , равен 0. Отсюда , то есть теорема Ферма утверждает, что касательная, проведённая в точке экстремума, горизонтальна (если эта касательная существует).

Доказательство теоремы Ферма. Если производная в точке экстремума не существует, то утверждение теоремы верно. Предположим, что производная существует. Рассмотрим два случая.

Пусть функция имеет в точке 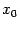максимум. Тогда при всех , поскольку . Если взять , то , и поэтому 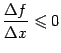. При вычислении производной мы переходим к пределу при в этом разностном отношении. При этом знак нестрогого неравенства сохраняется, когда мы берём предел справа:

Аналогично, при , , и поэтому . Отсюда, вычисляя предел слева, получаем:

Итак, выполняются два неравенства: и , что возможно лишь при .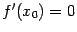

Пусть теперь функция имеет в точке 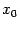минимум. Тогда при всех , поскольку . Если взять , то , и поэтому . Переходя к пределу при в разностном отношении, получаем:

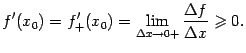
Аналогично, при , , и поэтому 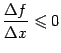. Вычисляя предел слева, получаем:

Из неравенств и получаем, что .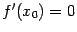

Билет 16:

Вопрос 1:Определение гиперболы. Вывод уравнения:

Определение. Гиперболой называется множество точек плоскости, для которых модуль разности расстояний от двух данных точек, называемых фокусами есть величина постоянная, меньшая расстояния между фокусами

y M(x, y) b r1 r2 x F1 a F2 c По определению r1 – r2= 2a. F1, F2 – фокусы гиперболы. F1F2 = 2c.

Выберем на гиперболе произвольную точку М(х, у). Тогда:

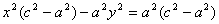
Обозначим с2 – а2 = b2 (геометрически эта величина – меньшая полуось) =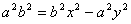

Получили каноническое уравнение гиперболы. Гипербола симметрична относительно середины отрезка, соединяющего фокусы и относительно осей координат. Ось 2а называется действительной осью гиперболы.

Ось 2b называется мнимой осью гиперболы. Гипербола имеет две асимптоты, уравнения которых

Вопрос 2: Теорема Ролля:

Теорема: Пусть функция дифференцируема на интервале 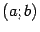, непрерывна в точках 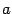и 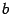и принимает в этих точках значение 0: . Тогда найдётся хотя бы одна точка , в которой .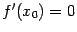

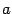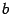Замечание: Это утверждение можно переформулировать так: между двумя корнями и дифференцируемой функции обязательно найдётся корень её производной 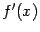(то есть точка , такая что 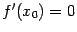). Условие 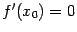означает, что касательная, проведённая к графику при , расположена горизонтально.

Заметим также, что теорема Ролля не утверждает, что корень 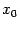- единственный корень производной на интервале 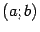; на этом интервале может находиться несколько корней производной.

Рис.5.4.Между двумя корнями дифференцируемой функции лежит хотя бы один корень её производной

Геометрический смысл:

Если крайние ординаты равны, то внутри 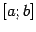найдется точка, в которой касательная будет параллельна оси абсцисс.

Доказательство теоремы Ролля. Так как при наших предположениях функция непрерывна на отрезке 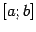, то она принимает своё максимальное значение и минимальное значение в некоторых точках и 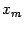этого отрезка.

Рассмотрим два случая. Если , то наибольшее и наименьшее значения функции совпадают, и, следовательно, функция постоянна на отрезке 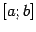: 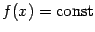. Значит, при всех , и в качестве 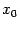в этом случае можно взять любую точку 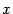интервала .

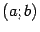Если же , то либо , либо отлично от 0 и, следовательно, либо точка , либо точка 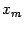не совпадает с концами отрезка 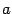и 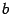, то есть лежит внутри интервала 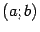. Пусть, для определённости, 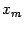- внутренняя точка интервала. Тогда, по теореме Ферма, , поскольку по предположению доказываемой теоремы, имеет производную во всех точках интервала 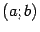и, следовательно, в точке 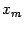. Итак, в этом случае точку 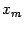можно взять в качестве искомой точки 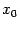: тогда .

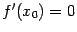Билет 17:

Вопрос 1: Определение параболы. Вывод уравнения:

Определение. Параболой называется множество точек плоскости, каждая из которых находится на одинаковом расстоянии от данной точки, называемой фокусом, и от данной прямой, называемой директрисой и не проходящей через фокус.

Расположим начало координат посередине между фокусом и директрисой.

А М(х, у)

О F x

p/2 p/2

Величина р (расстояние от фокуса до директрисы) называется параметром параболы. Выведем каноническое уравнение параболы.

Из геометрических соотношений: AM = MF; AM = x + p/2;

MF2 = y2 + (x – p/2)2

(x + p/2)2 = y2 + (x – p/2)2

x2 +xp + p2/4 = y2 + x2 – xp + p2/4

y2 = 2px

Уравнение директрисы: x = -p/2.

Вопрос 2: Теорема Коши:

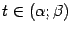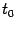Теорема: Пусть функции и дифференцируемы на интервале и непрерывны при и , причём при всех . Тогда в интервале найдётся такая точка , что

Геометрический смысл: Данные теоремы состоят в том, что внутри есть точка t₀, угловые коэффициенты в которой вычисляются по равенству:

Доказательство. Докажем сначала, что , то есть что дробь в левой части формулы имеет смысл. Действительно, для этой разности можно записать формулу конечных приращений:

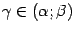при некотором . Но в правой части этой формулы оба множителя отличны от нуля.

Для доказательства теоремы введём вспомогательную функцию

Функция , очевидно, является дифференцируемой при всех 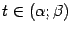и непрерывной в точках 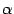и 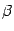, поскольку этими свойствами обладают функции и 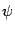. Кроме того, очевидно, что при получается . Покажем, что и :

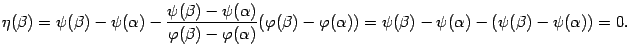
Значит, функция удовлетворяет на отрезке условиям теоремы Ролля. Поэтому существует такая точка , что .

Вычислим теперь производную функции :

Получаем, что

откуда получаем утверждение теоремы:

Замечание: Можно считать функци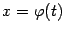и и координатами движущейся на плоскости точки, которая описывает линию , соединяющую начальную точку с конечной точкой .(Тогда уравнения и параметрически задают некоторую зависимость , графиком которой служит линия .)

Рис.5.6.Хорда параллельна некоторой касательной к кривой

Отношение , как нетрудно видеть из чертежа, задаёт тогда угловой коэффициент хорды, соединяющей точки и . В то же время, по формуле производной функции, заданной параметрически, имеем: . Значит, дробь - это угловой коэффициент касательной к линии в некоторой точке . Тем самым утверждение теоремы означает, с геометрической точки зрения, что на линии найдётся точка такая, что проведённая в этой точке касательная параллельна хорде, соединяющей крайние точки линии. Но это - то же самое утверждение, которое составляло геометрический смысл теоремы Лагранжа. Только в теореме Лагранжа линия была задана явной зависимостью 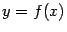, а в теореме Коши - зависимостью, заданной в параметрической форме.

Билет 18:

Вопрос 1: Понятие матрицы. Классификация матриц:

Определение. Матрицей размера mn, где m- число строк, n- число столбцов, называется таблица чисел, расположенных в определенном порядке. Эти числа называются элементами матрицы. Место каждого элемента однозначно определяется номером строки и столбца, на пересечении которых он находится. Элементы матрицы обозначаются aij, где i- номер строки, а j- номер столбца. А =