Матрица может состоять как из одной строки, так и из одного столбца. Вообще говоря, матрица может состоять даже из одного элемента.
Определение. Если число столбцов матрицы равно числу строк (m=n), то матрица называется квадратной.
Определение. Матрица вида:  = E, называется единичной матрицей.
= E, называется единичной матрицей.
Определение. Если amn = anm, то матрица называется симметрической. Пример. 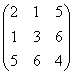 - симметрическая матрица
- симметрическая матрица
Определение. Квадратная матрица вида  называется диагональной матрицей.
называется диагональной матрицей.
Вопрос 2: Теорема Лагранжа:
Теорема: Пусть функция  дифференцируема на интервале
дифференцируема на интервале 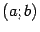 и непрерывна в точках
и непрерывна в точках 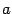 и
и 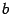 . Тогда найдётся такая точка
. Тогда найдётся такая точка  , что
, что 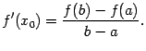
Геометрический смысл: Дадим сначала геометрическую иллюстрацию теоремы. Соединим конечные точки графика 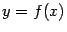 на отрезке
на отрезке 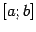 хордой. Конечные приращения
хордой. Конечные приращения 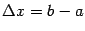 и
и 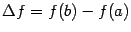 - это величины катетов треугольника, гипотенузой которого служит проведённая хорда.
- это величины катетов треугольника, гипотенузой которого служит проведённая хорда.

Рис.5.5.Касательная в некоторой точке параллельна хорде
Отношение конечных приращений 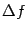 и
и 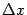 - это тангенс угла наклона хорды. Теорема утверждает, что к графику дифференцируемой функции можно провести в некоторой точке
- это тангенс угла наклона хорды. Теорема утверждает, что к графику дифференцируемой функции можно провести в некоторой точке 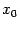 касательную, которая будет параллельна хорде, то есть угол наклона касательной
касательную, которая будет параллельна хорде, то есть угол наклона касательной 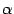 (
( 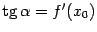 ) будет равен углу наклона хорды
) будет равен углу наклона хорды 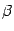 (
( 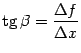 ). Но наличие такой касательной геометрически очевидно.
). Но наличие такой касательной геометрически очевидно.
Заметим, что проведённая хорда, соединяющая точки 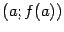 и
и 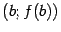 - это график линейной функции
- это график линейной функции 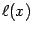 . Поскольку угловой коэффициент этой линейной функции равен, очевидно,
. Поскольку угловой коэффициент этой линейной функции равен, очевидно, 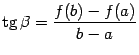 , то
, то 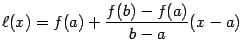
Доказательство теоремы Лагранжа. Сведём доказательство к применению теоремы Ролля. Для этого введём вспомогательную функцию 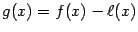 , то есть
, то есть
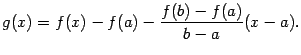
Заметим, что 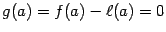 и
и 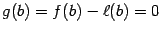 (по построению функции
(по построению функции 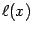 ). Так как линейная функция
). Так как линейная функция 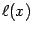 дифференцируема при всех
дифференцируема при всех 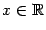 , то функция
, то функция 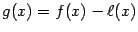 удовлетворяет, тем самым, всем свойствам, перечисленным в условии теоремы Ролля. Поэтому найдётся такая точка
удовлетворяет, тем самым, всем свойствам, перечисленным в условии теоремы Ролля. Поэтому найдётся такая точка  , что
, что 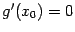 .
.
Заметим теперь, что
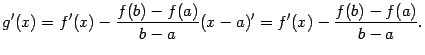
Значит, равенство 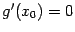 можно переписать в виде
можно переписать в виде
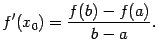
Из теоремы Лагранжа вытекает утверждение, обратное к тому, что производная постоянной есть 0, а именно:
Следствие: Пусть на интервале 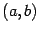 функция
функция  имеет производную
имеет производную 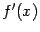 , тождественно равную 0:
, тождественно равную 0: 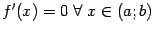 . Тогда
. Тогда 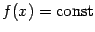 на интервале
на интервале 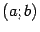 .
.
Доказательство. Заметим для начала, что непрерывность функции  в любой точке интервала
в любой точке интервала 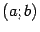 следует из дифференцируемости в этой точке. Значит, теорему Лагранжа можно применить к функции
следует из дифференцируемости в этой точке. Значит, теорему Лагранжа можно применить к функции  на любом отрезке
на любом отрезке 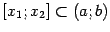 .
.
Возьмём любые две точки 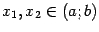 , такие что
, такие что 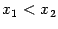 , и выпишем для функции
, и выпишем для функции  на отрезке
на отрезке 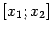 формулу конечных приращений:
формулу конечных приращений: 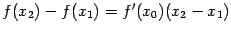 , при некотором
, при некотором 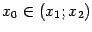 . Но в любой точке производная по предположению равна 0, в том числе
. Но в любой точке производная по предположению равна 0, в том числе 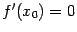 . Отсюда
. Отсюда 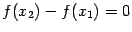 , или
, или 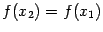 . Обозначим это общее значение через
. Обозначим это общее значение через 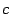 . Выбирая произвольно точку
. Выбирая произвольно точку 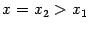 , получим, что
, получим, что 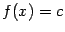 при всех
при всех 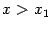 ; выбирая произвольно точку
; выбирая произвольно точку 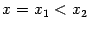 , - что
, - что 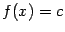 при всех
при всех 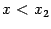 . Но это означает, что
. Но это означает, что 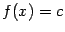 при всех
при всех  .
.
Билет 19:
Вопрос 1: Действия с матрицами:
Сложение и вычитание матриц сводится к соответствующим операциям над их элементами. Самым главным свойством этих операций является то, что они определены только для матриц одинакового размера. Таким образом, возможно определить операции сложения и вычитания матриц:
Определение. Суммой (разностью) матриц является матрица, элементами которой являются соответственно сумма (разность) элементов исходных матриц. cij = aij bij С = А + В = В + А. Операция умножения (деления) матрицы любого размера на произвольное число сводится к умножению (делению) каждого элемента матрицы на это число.  (А+В) =А В А() = А А Пример. Даны матрицы А =
(А+В) =А В А() = А А Пример. Даны матрицы А = 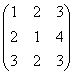 ; B =
; B =  , найти 2А + В. 2А =
, найти 2А + В. 2А = 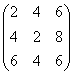 , 2А + В =
, 2А + В = 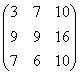 .
.
 2020-01-14
2020-01-14 149
149








