Элементарные преобразования

1) умножение строки на число, отличное от нуля;

2) прибавление к одной строке другой строки;

3) перестановка строк;

 4) вычеркивание (удаление) одной из одинаковых строк (столбцов);

5) транспонирование; Те же операции, применяемые для столбцов, также называются элементарными преобразованиями. С помощью элементарных преобразований можно к какой-либо строке или столбцу прибавить линейную комбинацию остальных строк (столбцов). 

 

Вопрос 2: Правило Лопиталя:

Теорема: (Правило Лопиталя для отношения бесконечно больших). Пусть и при и в некоторой проколотой окрестности , , 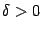существуют производные 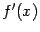и . Тогда, если существует предел отношения этих производных то существует и предел отношения самих функций, равный тому же числу:

Доказательство. Докажем, что оба предела совпадают, в предположении, что второй из них существует и оба не равны 0. Итак, пусть

где - некоторое число. Докажем, что тогда .

Рассмотрим вспомогательные функции

и

Тогда функции и - бесконечно малые при , непрерывные при ; их производные таковы:

Заметим теперь, что при

и

Из равенства получаем, что . Переходя к пределу в равенстве, получаем:

С другой стороны, применяя правило Лопиталя к бесконечно малым функциям и , получим:

откуда

Из этого равенства следует, что , что и требовалось доказать.

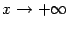Замечание: Немного изменив доказательство, мы получим, что правило Лопиталя для отношения двух бесконечно больших верно для односторонних пределов (при базах и ); сделав замену , выведем, что оно верно для пределов при базах , и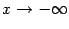

Замечание: Как и в основном случае отношения двух бесконечно малых при , все остальные варианты правила Лопиталя не универсальны: если предел отношения производных не существует, то это ещё не означает, что нет предела отношения исходных величин.

Билет 20:

Вопрос 1: Нахождение обратной матрицы:

 

Обратная матрица. Определим операцию деления матриц как операцию, обратную умножению.

Определение. Если существуют квадратные матрицы Х и А, удовлетворяющие условию: XA = AX = E, где Е - единичная матрица того же самого порядка, то матрица Х называется обратной к матрице А и обозначается А-1. Каждая квадратная матрица с определителем, не равным нулю имеет обратную матрицу и притом только одну. Рассмотрим общий подход к нахождению обратной матрицы. Исходя из определения произведения матриц, можно записать: AX = E  , i=(1,n), j=(1,n), eij = 0, i  j, eij = 1, i = j. Таким образом, получаем систему уравнений: , Решив эту систему, находим элементы матрицы Х.

 

Пример. Дана матрица А = , найти А-1. Таким образом, А-1= . Однако, такой способ не удобен при нахождении обратных матриц больших порядков, поэтому обычно применяют следующую формулу: , где Мji- дополнительный минор элемента аji матрицы А.

Пример. Дана матрица А = , найти А-1. det A = 4 - 6 = -2. M11=4; M12= 3; M21= 2; M22=1 x11= -2; x12= 1; x21= 3/2; x22= -1/2 Таким образом, А-1= .

 

Вопрос 2: Производные высших порядков:

Если функция дифференцируема при всех , то мы можем рассмотреть функцию , сопоставляющую каждой точке 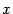значение производной 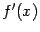. Эта функция называется производной функции , или первой производной от . (Иногда саму исходную функцию называют нулевой производной и обозначают тогда .) Функция , в свою очередь, может иметь производную во всех (или некоторых) точках 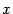интервала 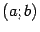, которую мы обозначим и назовём второй производной функции . Если предположить, что вторая производная существует во всех точках , то она может также иметь производную , называемую третьей производной функции , и т. д. Вообще, -й производной функции называется производная от предыдущей, -й производной :

если эта производная существует. -я производная называется также производной -го порядка, а её номер называется порядком производной.

При первую, вторую и третью производные принято обозначать штрихами: или ; при прочих - числом в скобках в верхнем индексе: или .

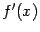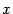Физический смысл производной второго порядка проясняется из того, что если первая производная задаёт мгновенную скорость изменения значений в момент времени , то вторая производная, то есть производная от 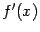, задаёт мгновенную скорость изменения значений мгновенной скорости, то есть ускорение значений . Следовательно, третья производная - это скорость изменения ускорения (или, что то же самое, ускорение изменения скорости, поскольку, как очевидно следует из определения, ).

Геометрический смысл второй производной связан с понятиями выпуклости и кривизны графика функции.

 

Билет 21:

Вопрос 1: Определители второго и третьего порядка:

Определитель квадратной матрицы будем обозначать или .

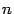Определение: Определителем квадратной матрицы второго порядка называется число . Определителем квадратной матрицы порядка , , называется число

где - определитель матрицы порядка , полученной из матрицы вычеркиванием первой строки и столбца с номером .

Замечание 1: Реальное вычисление определителей для матриц выше третьего порядка на основе определения используется в исключительных случаях. Как правило, вычисление ведется по другим алгоритмам.

Замечание 2: определитель есть функция, определенная на множестве квадратных матриц порядка 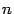и принимающая значения в множестве чисел.

Замечание 3: В литературе вместо термина "определитель" используется также термин "детерминант", имеющий тот же самый смысл. От слова "детерминант" и появилось обозначение .

Вопрос 2: Исследование участков монотонности функции:

Признак монотонности функции: Функция f(x) не убывает и не возоастает на промежутке X, если для любых X₁, X₂ X  из условия X₁ < X₂ следует неравенство

f(x₁)≤f(x₂) или f(x₁)≥f(x₂).

Если для тех же X из условия X₁ < X₂ следует неравенство f(x₁)<f(x₂) или f ( x ₁)> f ( x ₂), то функция f(x) называется возрастающей или убывающей на промежутке Х.

Теорема: Если функция дифференцируема на (a;b) и f’(x)≥0 или f’(x)≤0 на (a;b), то функция f(х) не убывает или не возрастает на (a;b).