Пусть Z = f(x,y);  ;
; 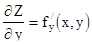 .
.
Изобразим Z = f(x,y) - получим некоторую поверхность.
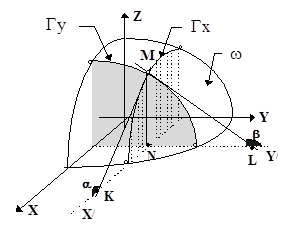
Рис. 13.1.
Возьмем точки М(х,у,z), N(x,y,0) - проекция точки М на плоскость ХоУ. Полагая у - const, мы получаем плоскую кривую Гx, представляющую собой сечение поверхности w соответствующей плоскостью, параллельной Оxz. Пусть МК - касательная к кривой Гx в точке М(х,у,z) и a - угол, образованный с положительным направлением оси Ох. Так как
 ,
,
на основании смысла обычной производной имеем  , аналогично
, аналогично  .
.
Билет 27:
Вопрос 1: Метод Жордана - Гаусса:
Метод Жордана - Гаусса является модификацией метода Гаусса. Назван в честь Гаусса и Жордана
Применяется для систем любого вида.
Система называется с базисом, если в каждом её уравнении присутствует неизвестное с коэффициентом +1, и она не присутствовала в других уравнениях (k=0), остальные переменные называются свободными.
Метод Жордана - Гаусса состоит в последовательном исключении неизвестных с помощью элементарных преобразований, в результате чего получается эквивалентная система базисов.
АЛГОРИТМ РЕШЕНИЯ:
1. Записываем все данные в таблицу, слева коэффициенты, а справа правые части. И выбираем ключевой элемент. Его можно выбирать только из коэффициентов неизвестных неравных 0.
2. Преобразуем ключевую строку. Для этого все числа строки делим на выбранный ключевой1 элемент.
3. Преобразуем не ключевые строки. Из каждого числа проводи два перпендикуляра, числа на концах перпендикуляров умножаем и полученное произведение вычитаем из выбранного числа.
4. Появление нулевой строки. Что говорит о том, что данное уравнение было следствием других, и нулевую строку вычеркиваем.
5. Окончание преобразования. Возможны случаи:
· Если количество выбранных ключевых элементов равно числу строк, то есть числу уравнений, то данное уравнение имеет единственное решение.
· Если число ключевых элементов меньше числа переменных, то данная система уравнений имеет бесконечное множество решений.
· Если в результате преобразований получилась строка, на месте коэффициентов 0, а в правой части число, то это говорит о том, что система решений не имеет, то есть несовместна.
Рассмотрим пример:

| X1 | X2 | X3 | bi | |
| 1 | 1 | 1 | 0 | |
| 4 | 2 | 1 | 1 | |
| 9 | 3 | 1 | 3 | |
| 1 | 1 | 1 | 0 | |
| 3 | 1 | 0 | 1 | |
| 8 | 2 | 0 | 2 | |
| -2 | 0 | 1 | -1 | |
| 3 | 1 | 0 | 1 | |
| 2 | 0 | 0 | 0 | /2 |
| 0 | 0 | 1 | -1 | |
| 0 | 1 | 0 | 1 | |
| 1 | 0 | 0 | 0 |
Ответ:
X1=-1
X2=1
X3=0
Вопрос 2: Частные производные высших порядков:
Пусть функция z=f(M) имеет частные производные fx’(x;y) и fy’(x;y) (они называются частными производными первого порядка) в каждой точке некоторой окрестности точки М. Если fx’(x;y) и fy’(x;y) имеют в точке М частные производные по переменным х и у, то они называются частными производными второго порядка от функции f(M) в этой точке и обозначаются следующими символами:
1. 
2. 
3. 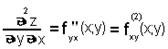
4. 
Частные производные второго порядка вида  ,
,  называются смешанными частными производными.
называются смешанными частными производными.
Частные производные третье порядка определяются как частные производные от частных производных второго порядка и так далее.
Билет 28:
Вопрос 1: Линейная балансовая модель:
Изучение балансовых моделей, представляющих собой одно из важнейших направлений и экономико-математических исследований, должно служить объектом изучения отдельной дисциплины. Наша цель проиллюстрировать на примере балансовых расчетов применение основных понятий линейной алгебры.
Линейная балансовая модель:
Пусть рассматривается экономическая система, состоящая из n взаимосвязанных отраслей производства. Продукция каждой отрасли частично идет на внешнее потребление конечный продукт, а частично используется в качестве сырья, полуфабрикатов или других средств производства в других отраслях, в том числе и в данной. Эту часть продукции называют производственным потреблением. Поэтому каждая из рассматриваемых отраслей выступает и как производитель продукции первый столбец таблицы 1 и как ее потребитель первая строка таблицы 1.
Обозначим через xi валовый выпуск продукции iй отрасли за планируемый период и через yi конечный продукт, идущий на внешнее для рассматриваемой системы потребление средства производства других экономических систем, потребление населения, образование запасов и т.д..
Таким образом, разность xi yi составляет часть продукции iй отрасли, предназначенную для внутрипроизводственного потребления. Будем в дальнейшем полагать, что баланс составляется не в натуральном, а в стоимостном разрезе.
Обозначим через xik часть продукции iй отрасли, которая потребляется kй отраслью, для обеспечения выпуска ее продукции в размере хk.
Таблица 1
потребление итого на конечный валовый
отрас. внутре продукт выпуск
производ. уi хi
1 2 k n потребление
отрас. хik
1 х11 х12 х1k х1n х1k у1 х1
2 х21 х22 х2k х2n х2k у2
Вопрос 2: Градиент:
Определение: Градиентом функции z=(M) в точке М(х;у) называется вектор, координаты которого равны соответствующим частным производным 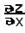 и
и  , взятым в точке М(х;у).
, взятым в точке М(х;у).
Обозначение: gradz= 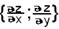 .
.
Для трех переменных функции u=f(x;y;z) градиент будет: gradu(ux’(M0);uy’(M0);uz’(M0))
Градиенты используются в задачах оптимизации, так как градиент направление наискорейшего роста функции.
Билет 29:
Вопрос 1: Определение ранга матрицы. Теорема Кронекера-Капелли:
Определение: Пусть дана матрица  размеров
размеров 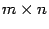 и число
и число  , не превосходящее наименьшего из чисел
, не превосходящее наименьшего из чисел 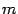 и
и 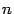 :
: 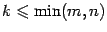 . Выберем произвольно
. Выберем произвольно  строк матрицы
строк матрицы  и
и  столбцов (номера строк могут отличаться от номеров столбцов). Определитель матрицы, составленной из элементов, стоящих на пересечении выбранных
столбцов (номера строк могут отличаться от номеров столбцов). Определитель матрицы, составленной из элементов, стоящих на пересечении выбранных  строк и
строк и  столбцов, называется минором порядка
столбцов, называется минором порядка  матрицы
матрицы  .
.
Пример: Пусть  .
.
Минором первого порядка является любой элемент матрицы. Так 2, -5,-4 - миноры первого порядка.
Миноры второго порядка:
возьмем строки 1, 2, столбцы 1, 2, получим минор  ;
;
возьмем строки 1, 3, столбцы 2, 4, получим минор  ;
;
возьмем строки 2, 3, столбцы 1, 4, получим минор 
Миноры третьего порядка: строки здесь можно выбрать только одним способом, возьмем столбцы 1, 3, 4, получим минор 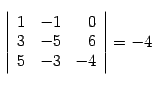 ;
;
возьмем столбцы 1, 2, 3, получим минор  .
.
Свойство 1: Если все миноры матрицы  порядка
порядка  равны нулю, то все миноры порядка
равны нулю, то все миноры порядка  , если такие существуют, тоже равны нулю.
, если такие существуют, тоже равны нулю.
Свойство 2: При транспонировании матрицы ее ранг не меняется, то есть  .
.
Свойство 3: Пусть ранг матрицы равен  . Тогда любой минор порядка
. Тогда любой минор порядка  , отличный от нуля, называется базисным минором.
, отличный от нуля, называется базисным минором.
Свойство 4: Система столбцов (строк) называется линейно зависимой, если существует такой набор коэффициентов, из которых хотя бы один отличен от нуля, что линейная комбинация столбцов (строк) с этими коэффициентами будет равна нулю.
Свойство 5: Система столбцов (строк) является линейно независимой, если из равенства нулю линейной комбинации этих столбцов (строк) следует, что все коэффициенты этой линейной комбинации равны нулю.
Свойство 6: Предложение 14.25 Система столбцов (строк) является линейно зависимой тогда и только тогда, когда один из столбцов (одна из строк) является линейной комбинацией других столбцов (строк) этой системы.
Свойство 7: Ранг матрицы равен максимальному числу ее столбцов, образующих линейно независимую систему.
Свойство 8: Ранг матрицы равен максимальному числу ее строк, образующих линейно независимую систему.
Свойство 9: Если определитель матрицы равен нулю, то один из его столбцов (одна из строк) является линейной комбинацией остальных столбцов (строк).
Свойство 10: При элементарных преобразованиях ранг матрицы не меняется.
Теорема Кронекера – Капели: Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг основной матрицы равен рангу расширенной матрицы.
Доказательство.
1) Если решение существует, то столбец свободных членов есть линейная комбинация столбцов матрицы А, а значит добавление этого столбца в матрицу, т.е. переход АА* не изменяют ранга.
2) Если RgA = RgA*, то это означает, что они имеют один и тот же базисный минор. Столбец свободных членов – линейная комбинация столбцов базисного минора, те верна запись, приведенная выше.
Пример. Определить совместность системы линейных уравнений:

A = 
~  .
.  RgA = 2.
RgA = 2.
A* = 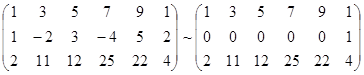 RgA* = 3.
RgA* = 3.
Система несовместна.
Вопрос 2: Производная по направлению:
Пусть z=f(M) – функция, определенная в некоторой окрестности точки М(х;у);  ={соs
={соs  ;cos
;cos  ) – единичный вектор; L – направленная прямая, проходящая через точку М; М1(х+
) – единичный вектор; L – направленная прямая, проходящая через точку М; М1(х+ 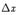 ;у+
;у+  ) - точка на прямой L;
) - точка на прямой L; 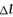 - величина отрезка ММ1;
- величина отрезка ММ1;  - f(x;y) – приращение функции f(M) в точке М(х;у).
- f(x;y) – приращение функции f(M) в точке М(х;у).
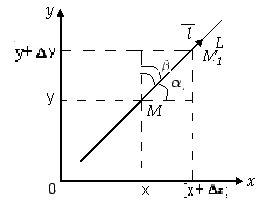
Определение: Предел отношения  при
при  (М1
(М1  М), если он существует, называется производной функции z=f(M) в точке М(х;у) по направлению вектора
М), если он существует, называется производной функции z=f(M) в точке М(х;у) по направлению вектора  и обозначается
и обозначается  , то есть
, то есть  .
.
Если функция f(M) дифференцируема в точке М(х;у), то в точке М(х;у) существует производная по любому направлению  , исходящему из М; вычисляется по следующей формуле:
, исходящему из М; вычисляется по следующей формуле:
 , где соs
, где соs  и cos
и cos  - направляющей косинусы вектора
- направляющей косинусы вектора  .
.
Билет 30:
Вопрос 1: Определение функции. Способы задания функции:
Отображе́ние или фу́нкция (лат. functio — исполнение, осуществление) — одно из основных понятий математики, выражающее зависимость одной величины от другой.
Способы задания функции:
1. Словесный
у равен целой части от х. ( )
)
2. Аналитический
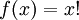
3. Графический
С помощью графика.
4. Табличный
Функция задается таблицей значений
Вопрос 2: Экстремумы функции нескольких переменных:
 2020-01-14
2020-01-14 161
161








