Обратной тригонометрической функцией y = arcsin x, называют дугу (угол) у, взятую в отрезке  , синус которой равен x.
, синус которой равен x.
y = arcsin x и sin y = x - равенства эквиваленты
y = arccos x и cos y = x – равенства эквиваленты
y = arctg x и tq y = x - равенства эквиваленты
y = arcctg x и ctg y = x – равенства эквиваленты
Значение тригонометрических функций некоторых углов
| α | 00 | 300 | 450 | 600 | 900 | 1200 | 1800 | 2700 | 3600 |
| sin α | 0 | 
| 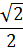
| 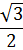
| 1 | 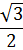
| 0 | -1 | 0 |
| cos α | 1 | 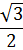
| 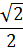
| 
| 0 | 
| -1 | 0 | 1 |
| tg α | 0 | 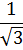
| 1 | 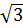
| ∞ | 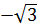
| 0 | ∞ | 0 |
| ctg α | ∞ | 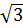
| 1 | 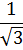
| 0 | 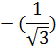
| ∞ | 0 | ∞ |
| sec α | 1 | 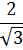
| 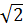
| 2 | ∞ | -2 | -1 | ∞ | 1 |
| cosec α | ∞ | 2 | 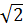
| 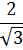
| 1 | 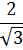
| ∞ | -1 | ∞ |
Геометрия
Треугольник
Треугольник – это геометрическая фигура, состоящая из трех точек, попарно соединенных и не лежащих на одной прямой.
Равносторонний треугольник - треугольник, у которого все стороны равны
c-сторона;
H -высота;
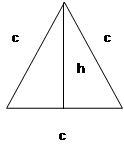 S- площадь.
S- площадь.
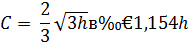

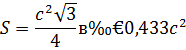
Равнобедренный треугольник - треугольник, у которого две боковые стороны равны.
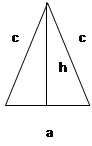 В равнобедренном треугольнике медиана, проведенная из вершины к основанию, является высотой и биссектрисой.
В равнобедренном треугольнике медиана, проведенная из вершины к основанию, является высотой и биссектрисой.
Прямоугольный треугольник
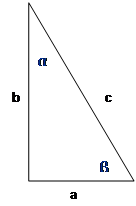 |
а,b-катеты;
с-гипотенуза;
α,β-острые углы;
с2=а2+b2;
α+β=90˚;
S-площадь.
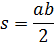
Решение прямоугольных треугольников
a,b - катеты c - гипотенуза, < α + < β = 900 (острые углы)
a= c sin α; a = b tg α; b = c cos α; b =a ctg α; b = a tg β
c = a/ sin α; c = b / sin β;
a2 + b2 = c2 - теорема Пифагора
Основные теоремы и формулы о соотношениях между элементами треугольников
Сумма внутренних углов треугольника: A+B+C= π = 1800
Теорема синусов: 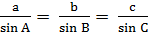
Теорема косинусов: a2 = b2 + c2 – 2bc cos A
Квадрат
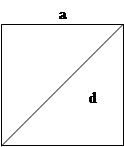 |
Квадрат – прямоугольник, у которого все стороны равны.
a-сторона;
d-диагональ;
S-площадь.
S = a2
Ромб
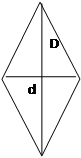 Ромб – параллелограмм, у которого все стороны равны.
Ромб – параллелограмм, у которого все стороны равны.
с-сторона;
D-большая диагональ;
d- малая диагональ;
S-площадь.

Трапеция
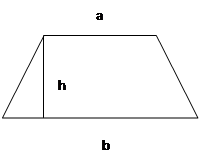 Трапеция – четырехугольник, две противоположные стороны которого параллельны, а две другие не параллельны.
Трапеция – четырехугольник, две противоположные стороны которого параллельны, а две другие не параллельны.
a,b-параллельные стороны, или основания;
h-высота;
S-площадь.
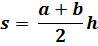
Правильный n-угольник
Правильный многоугольник – многоугольник, у которого все стороны и углы равны.
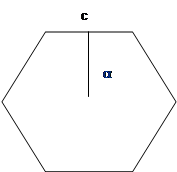 |
с-сторона;
α-апофема
Апофема - перпендикуляр, проведенный
из центра многоугольника.
S-площадь.

Сторона αn правильного вписанного многоугольника
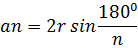
r-радиус окружности.
Круг
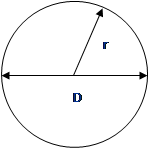 С-длина окружности;
С-длина окружности;
d-диаметр;
r-радиус;
S-площадь.
С=πd≈3,142d;
С=2πr≈6,283;
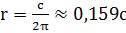
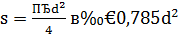
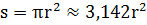
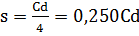
| Часть круга | Длина дуги | Площадь |
| ½ круга ¼ круга ⅙ круга | 3,142r 1,571r 1,047r | 1,571 r2 0,785 r2 0,525 r2 |
Круговое кольцо
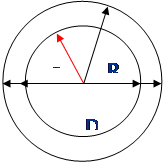 D-большой диаметр;
D-большой диаметр;
d- малый диаметр;
R - большой радиус;
r - малый радиус;
S – площадь
δ = D - d.
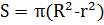

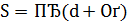
Призма

h-высота;
p- периметр оснований;
V-объем;
S-площадь основания;
Sбок - боковая поверхность.
V= Sh;
Sбок =ph.
Пирамида правильная
α – апофема;
 h-высота;
h-высота;
ρ-периметр оснований;
V-объем;
S-площадь оснований;
Sбок –боковая поверхность.
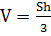 ;
;
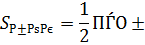
Усеченная пирамида
α – апофема;
h-высота;
p1, p2 –периметры оснований;
V- объем;
S1, S2 –площади нижнего и верхнего оснований;
Sбок –боковая поверхность.
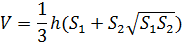
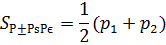
Цилиндр

h-высота;
r- радиус основания;
d-диаметр основания;
V-объем;
S-площадь основания;
Sбок –боковая поверхность.
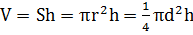
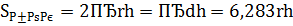
1.5.12 Конус
С-длина окружности основания;
 d-диаметр;
d-диаметр;
r-радиус;
L-образующая конуса;
h-высота;
V-объем;
S-площадь основания;
Sбок –боковая поверхность.
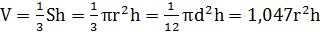

Усеченный конус
h-высота усеченного конуса;
H-высота полного конуса;
r-радиус малого основания;
R-радиус большого основания;
d-диаметр малого основания;
D-диаметр большого основания;
L-образующая усеченного конуса;
V-объем;
Sбок –боковая поверхность.

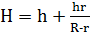
 1.5.13 Шар
1.5.13 Шар
D, R-диаметр и радиус шара;
r1, r2-радиусы оснований;
h - высота.
| Поверхность | Объем |
| 4πR2; πD2. | 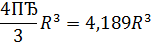
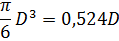
|
| Шаровой сегмент | |
| 2πRh; π(r2 + h2) | 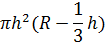
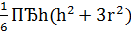
|
| Шаровой сектор | |
| πR(r+2h) | 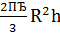
|
 2020-01-14
2020-01-14 141
141








